Предмет: Геометрия,
автор: 19607
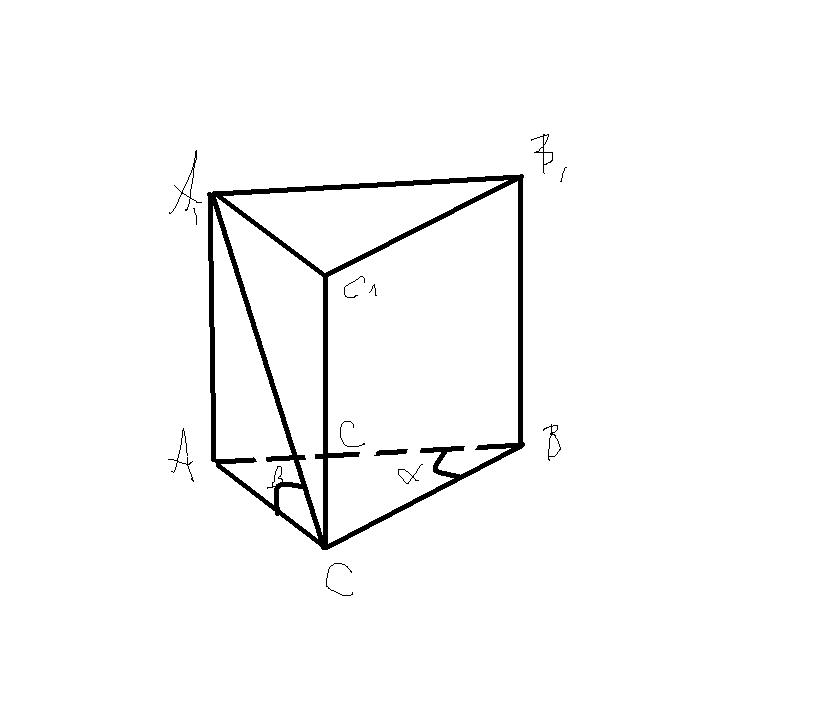
Основание прямой призмы-прямоугольный треугольник с гипотенузой с и астрым углом альфа.Диагональ боковой грани, содержащей катет,протеволежащий углу альфа, наклонена к пл-сти основания под углом бета.Найдитеобъём призмы.
Ответы
Автор ответа:
0
Пусть - данная пряммая призма с основанием ABC (прямоугольным треугольником с пряммым углом С), AB=c, угол
;
угол
Катеты треугольника АВС равны
Высота призмы равна
Площадь основания равна
Обьем призмы равен
Приложения:
Похожие вопросы
Предмет: Математика,
автор: ionhll668
Предмет: Математика,
автор: Lesha1222
Предмет: Алгебра,
автор: ilnaragybaj40
Предмет: Математика,
автор: Nataliadzr