Question

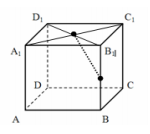
В  прямоугольном  параллелепипеде АВСD$A_{1} B_{1} C_{1} D_{1}$
 АВ=6, ВС=17, С$C_{1}$=6. Найдите расстояние 
от  середины  ребра  В$B_{1}$  до  точки  пересечения  диагоналей 
верхнего основания параллелепипеда.

Answer 1

Введем систему координат с началом в точке A, ось X направим по AB, Y - по AD, Z - по A$A_{1}$. Тогда точка пересечения диагоналей 
верхнего основания параллелепипеда будет иметь координаты $(3, \frac{17}{2},6)$, середина ребра B$B_{1}$ - $(6,0,3)$. Осталось применить формулу для расстояния между точками $\sqrt{(6-3)^{2}+(0- \frac{17}{2})^{2} +(3-6)^{2}}= \sqrt{ \frac{289+36+36}{4} }= \sqrt{ \frac{361}{4} }= \frac{19}{2}$