Предмет: Алгебра,
автор: Аноним
Помогите, пожалуйста с заданием.
Приложения:
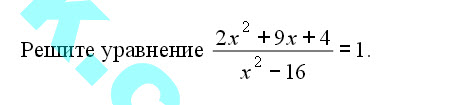
Ответы
Автор ответа:
0
Ответ:
Автор ответа:
0
(2х²+9х+4)/(х²-16)=(х²-16)/х²-16
(x²+9x+20)/(x²-16=)0
ОДЗ:
x²-16≠0
x²≠16
x≠4
x≠-4
x²+9x+20=0
D=81-80=1
x1=(-9+1)/2=-4 неудовлетворяет условию ОДЗ х≠-4
x2=(-9-1)/2=-5
Ответ:-5
(x²+9x+20)/(x²-16=)0
ОДЗ:
x²-16≠0
x²≠16
x≠4
x≠-4
x²+9x+20=0
D=81-80=1
x1=(-9+1)/2=-4 неудовлетворяет условию ОДЗ х≠-4
x2=(-9-1)/2=-5
Ответ:-5
Похожие вопросы
Предмет: Русский язык,
автор: bogdalla
Предмет: Окружающий мир,
автор: настятруш3467944
Предмет: Русский язык,
автор: 6yJIko
Предмет: Русский язык,
автор: Аноним
Предмет: Қазақ тiлi,
автор: zhalgas5454