Предмет: Алгебра,
автор: deftcat
Решить уравнение помогите, пожалуйста! :)
Приложения:
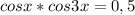
Ответы
Автор ответа:
0
cosx*cos3x=0,5 cos3x=cosx(4cos²x - 3)
cosx*cosx(4cos²x - 3) =1/2
cosx*cos3x=0,5 , но т.к . cos3x=cosx(4cos²x - 3)
[ cos3x=cos(2x+x)=cos2x*cosx-sin2x*sinx=cosx(2cos²x-1)-2sin²x*cosx)= ... ]
то cos²x(4cos²x - 3)=1/2 <==>2cos²x(4cos²x - 3)=1, обозн. t = cos²x ≥ 0
получаем квадратное уравнение
8t² - 6t -1=0 D/4=3² + 8=17
t1=(3+√17)/8 , t2=( 3- √17)/8 <0 не является решением уравнения
cos²x = (3+√17)/8 и==> (1+cos2x)/2 =(3+√17)/8 ==> 1+cos2x=(3+√17)/4
cos2x=(3+√17)/4 - 1 = (√17 -1)/4
2x =(+/-)arccos(√17 -1)/4+2π*k, k∈Z
x =(+/-)arccos(√17 -1)/8 +π*k, k∈Z (k целое число)
ответ : x =(+/-)arccos(√17 -1)/8 +π*k, k∈Z
ответ (+/-)arccos(√17 -1)/8 +π*k, k∈Z (целоое число)
cosx*cosx(4cos²x - 3) =1/2
cosx*cos3x=0,5 , но т.к . cos3x=cosx(4cos²x - 3)
[ cos3x=cos(2x+x)=cos2x*cosx-sin2x*sinx=cosx(2cos²x-1)-2sin²x*cosx)= ... ]
то cos²x(4cos²x - 3)=1/2 <==>2cos²x(4cos²x - 3)=1, обозн. t = cos²x ≥ 0
получаем квадратное уравнение
8t² - 6t -1=0 D/4=3² + 8=17
t1=(3+√17)/8 , t2=( 3- √17)/8 <0 не является решением уравнения
cos²x = (3+√17)/8 и==> (1+cos2x)/2 =(3+√17)/8 ==> 1+cos2x=(3+√17)/4
cos2x=(3+√17)/4 - 1 = (√17 -1)/4
2x =(+/-)arccos(√17 -1)/4+2π*k, k∈Z
x =(+/-)arccos(√17 -1)/8 +π*k, k∈Z (k целое число)
ответ : x =(+/-)arccos(√17 -1)/8 +π*k, k∈Z
ответ (+/-)arccos(√17 -1)/8 +π*k, k∈Z (целоое число)
Похожие вопросы
Предмет: Русский язык,
автор: xXstrangerXx1
Предмет: Английский язык,
автор: raccoon098
Предмет: Русский язык,
автор: kat898720
Предмет: Математика,
автор: Dias210707
Предмет: Математика,
автор: Koroleva347388