Предмет: Алгебра,
автор: pinosol03
Срочно!! очень прошу! Задание из ЕГЭ (С3) ! достаточно сделать первые несколько шагов, дальше я сама!!! заранее благодарю, вот задание
Приложения:
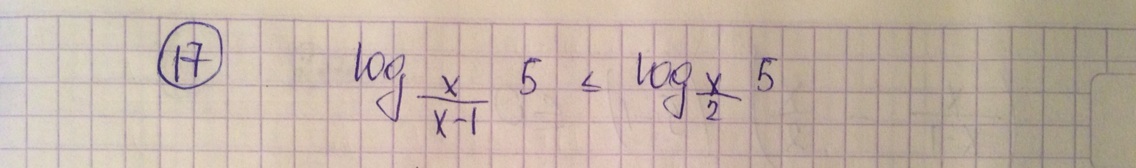
Ответы
Автор ответа:
1
1) Записать ОДЗ:







x∈(1;2)U(2;+бесконечность)
2) Упростим выражение:

Числители одинаковые, значит та дробь меньше, у которой знаменатель больше.




a)

x∈(1;3]
b)

x∈(-бесконечность;0)
3) Наложим на полученное решение условие ОДЗ, получим:
x∈(1;2)U(2;3]
Ответ: x∈(1;2)U(2;3]
x∈(1;2)U(2;+бесконечность)
2) Упростим выражение:
Числители одинаковые, значит та дробь меньше, у которой знаменатель больше.
a)
x∈(1;3]
b)
x∈(-бесконечность;0)
3) Наложим на полученное решение условие ОДЗ, получим:
x∈(1;2)U(2;3]
Ответ: x∈(1;2)U(2;3]
Похожие вопросы
Предмет: Английский язык,
автор: Yanfxbjkj
Предмет: Английский язык,
автор: margaritavladim
Предмет: Английский язык,
автор: asaliyakazoxssu7
Предмет: Математика,
автор: karapetyanlusine2005