Предмет: Геометрия,
автор: Тахминa
Прямые a и b лежат в параллельных плоскостях альфа и бета. Докажите, что эти прямые могут быть параллельными скрещивающимися?
Kristallik20:
Какой класс?
И каким должен быть рисунок, нужен ли он?
10
Да рисунок нужен
В общем, подойдет тебе или нет, не знаю. Я добавлю решение, если нет, то нет.)
Ответы
Автор ответа:
1
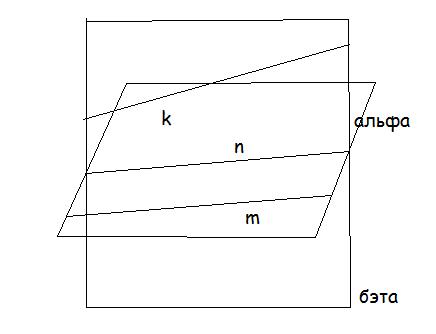
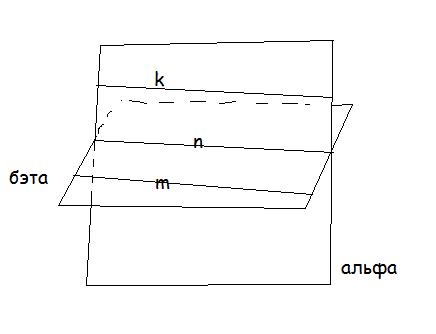
б)n - прямая пересечения плоскостей, m||n и принадлежит одной плоскости, k не параллельна n и принадлежит другой плоскости. Если k||m, то по свойству транзитивности k||n, противоречие, значит k не параллельна m. С другой стороны k и n не пересекаются, значит они скрещивающиеся. Подходит?
а) n - прямая пресечения плоскостей, m||n и принадлежит одной плоскости, а k||n и принадлежит другой плоскости, а тогда по свойству транзитивности m||n.
а) n - прямая пресечения плоскостей, m||n и принадлежит одной плоскости, а k||n и принадлежит другой плоскости, а тогда по свойству транзитивности m||n.
Приложения:
Про параллельные еще? Это подходит?
В общем, под а тоже написала)
Похожие вопросы
Предмет: Русский язык,
автор: zoandij
Предмет: Русский язык,
автор: ярик448
Предмет: Русский язык,
автор: полина6671
Предмет: Физика,
автор: TabLeToChA57