Question

В прямоугольном треугольнике биссектриса прямого угла делит гипотенузу в отношении 1:5. В каком отношении делит гипотенузу опущенная на неё высота?

Answer 1

 Биссектриса угла треугольника делит противоположную сторону в отношении прилежащих сторон. 
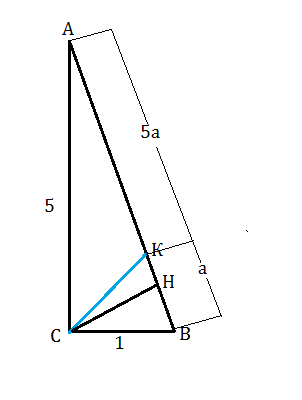
Пусть дан треугольник АВС, С=90º.СК-биссектриса, СН - высота. 
Так как отношение ВК:КА=1:5, то ВС:СА=1:5 
Из этого отношения можно принять СВ=1,СА=5 
По т.Пифагора АВ=√(AC²+BC²)=√26 
–Катет есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу. 
СВ²=АВ*ВН 
Примем ВН=х 
1²=(√26)*х 
х=1/√26 
BH=1/√26  
Тогда АН=АВ-ВИН=√26-(1/√26)=25/√26 
BH:AH=(25/√26):(1/√26)=25:1