Предмет: Геометрия,
автор: Кудряшка25
Помогите с задачей, пожалуйста.
В параллелограмме одна из диагоналей равна 6 см и образует со сторонами параллелограмма углы 45 и 60 градусов. Найдите высоты параллелограмма.
Заранее спасибо.
Ответы
Автор ответа:
0
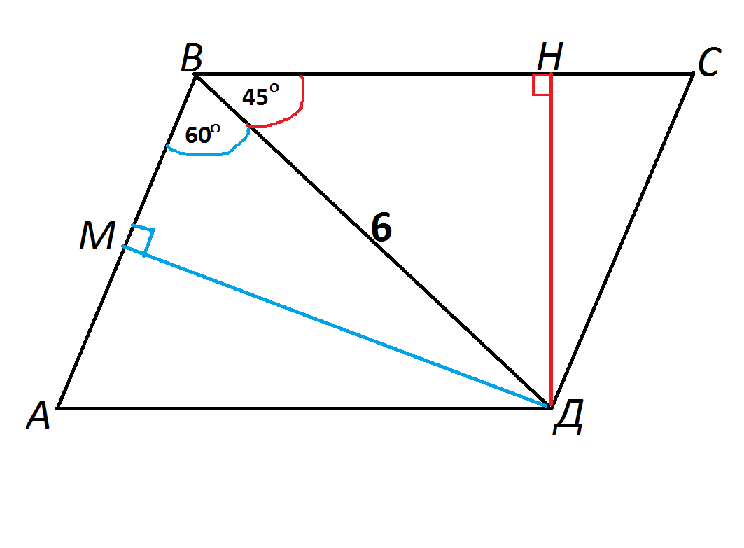
Пусть дан параллелограмм АВСД.
Тупой угол при вершине В параллелограмма равен 60°+45°.
Т.е. угол АВД=60°, угол СВД=45°
Проведем высоту ДН из угла Д к ВС.
Она образует прямоугольный равнобедренный треугольник с катетами ВН и ДН и гипотенузой ВД.
ДН=ВД*sin 45°=6*√2):2=3√2 см
Высота ДМ из Д к АВ образует с диагональю ВД прямоугольный треугольник ДМВ с острым углом МВД= 60° и гипотенузой ВД=6 см
ДМ=ВД*sin 60°=6*√3):2=3√3 см
Ответ: Высоты равны 3√2 см и 3√3 см.
Тупой угол при вершине В параллелограмма равен 60°+45°.
Т.е. угол АВД=60°, угол СВД=45°
Проведем высоту ДН из угла Д к ВС.
Она образует прямоугольный равнобедренный треугольник с катетами ВН и ДН и гипотенузой ВД.
ДН=ВД*sin 45°=6*√2):2=3√2 см
Высота ДМ из Д к АВ образует с диагональю ВД прямоугольный треугольник ДМВ с острым углом МВД= 60° и гипотенузой ВД=6 см
ДМ=ВД*sin 60°=6*√3):2=3√3 см
Ответ: Высоты равны 3√2 см и 3√3 см.
Приложения:
Автор ответа:
0
задачу 9 класс решишь?
Похожие вопросы
Предмет: Алгебра,
автор: Аноним
Предмет: Қазақ тiлi,
автор: gabdullinanoni
Предмет: Физика,
автор: evgeniycherevko29
Предмет: История,
автор: трипятница
Предмет: История,
автор: Ксенька587