Question

РЕБЯТКИ ПОМОГИТЕ РЕШИТЬ ПОЖАЛУЙСТА КРОМЕ 4 И 6 ЗАДАНИЙ

Answer 1

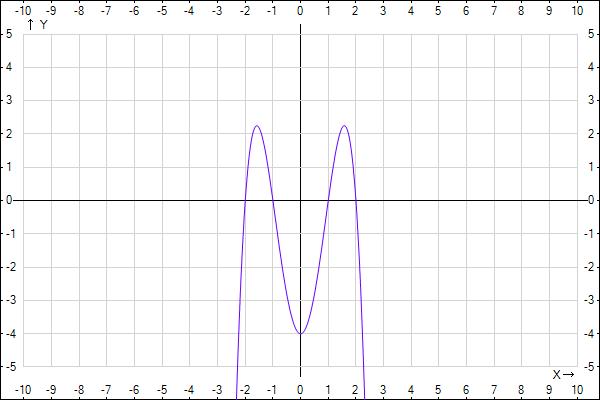
1/ Исследовать функцию и построить график

$y=-x^4+5x^2-4=-(x^2-1)(x^2-4)=-(x-1)(x+1)(x-2)(x+2);$

Область определения: область действительных чисел, так как функция - многочлен 4-й степени без ограничений на х,

$D(y)=R=(-infty; infty);$

Область значений:

Периодичность: непериодична как многочлен

Четность: функция четная (ООФ симметричина относительно точки х=0)

$y(-x)=-(-x)^4+5(-x)^2-4=-x^4+5x^2-4=y(x)$

Точки пересечения с осью Ох(y=0): 

-(x-1)(x+1)(x-2)(x+2)=0;

(1;0); (-1;0); (-2;0); (2;0)

Точки пересечения с осью Оy(x=0)

y=-0^4+5*0^2-4=-4;

(0;-4)

Точки экстремума

$y'=-4x^3+10x;\ y'=0;\ -4x^3+10x=0;\ 2x(x^2-5)=0;\ x_1=0; x_2=sqrt{5}; x_3=-sqrt{5};$

+[-корень(5)] -  [0] + [корень(5)] -

значит точка x=0 - точка минимуму

точки $<strong><var>x=^+_-sqrt{5}</var></strong>$ - точки максимума

Промежутки возростания $(-infty;-sqrt{5}) cup (0;sqrt{5})$

Промежутки убывания $(-sqrt{5};0) cup (sqrt{5}; +infty)$

Точки перегиб$y''=-12x^2+10;\ y''=0;\ -12x^2+10=0;\ -2(6x^2-5)=0;\ x_1=-frac{5}{6}; x_2=frac{5}{6}$

-[-корень(5/6)] +[корень(5/6)] -

значит функция выпукла на $-frac{5}{6};frac{5}{6}$

вогнута на $(-infty;<var>-frac{5}{6}) cup (frac{5}{6}; +infty)</var>$

Асимптоты: не имеет, как  многочлен

график во вложении.

 

$int{3x^5+frac{3}{x^3}+sqrt[4] x+3}, dx=\ int{3x^5}, dx+int frac{3}{x^3}}, dx+int{sqrt[4] x}, dx+int{3}, dx=\ 3int{x^5}, dx+3int x^{-3}, dx+int{x^{frac{1}{4}}}, dx+int{3}, dx=\ frac{3x^6}{6}-frac{3}{2x^2}+frac{4}{3 sqrt[4] {x^3}}+3x+C$

 

$int {sin x+frac{1}{cos^2 x} }, dx=\ int {sin x}, dx+int {frac{1}{cos^2 x} }, dx=\ -cos x+tg x+C$

 

$intlimits^1_8 sqrt[3] x-frac{2}{3}x} , dx =\ frac{3}{4} xsqrt[3] x-frac{x^2}{3} | limits^1_8 = frac{3}{4} 8*sqrt[3] 8-frac{8^2}{3} -frac{3}{4} 1*sqrt[3]1-frac{1^2}{3} =\ 12-frac{64}{3}-0.75-frac{1}{3}=frac{45}{4}-frac{65}{3}=frac{-125}{12}$

 

$x^2dy-(2xy+3y)dx=0; x_0=y_0=1;\ x^2dy-y(2x+3)dx=0;\ x^2dy=y(2x+3)dx;\ frac{(2x+3)dx}{x^2}=frac{dy}{y};\ frac{d(x^2+3)}{x^2}=frac{dy}{y};\ ln |x^2+3|+c=|y|;\ y=c(x^2+3);\ 1=c(1^2+3);\ c=0.25;\ y=0.25(x^2+3)=0.25x^2+0.75$

 

$z=2(cos frac{4pi}{3}+i*sin frac{4 pi}{3})=\ 2*(-cos frac{pi}{3}-i*sin frac{pi}{3})=\ 2*(-frac{1}{2}-i*frac{sqrt{3}}{2})=\ -1-sqrt{3}i$

 

Рассмотрим

$lim_{n to infty}frac{a_{n+1}}{a_n}=\ lim_{n to infty}frac{frac{3(n+1)^2}{2^{n+1}}}{frac{3n^2}{2^n}}=\ lim_{n to infty} frac{(n+1)^2 *2^n}{n^2*2*2^n}}=\ lim_{n to infty}2*(1+frac{1}{n})^2=\ 2*(1+0)^2=2>1$

за признаком Даламбера ряд расбегается