Предмет: Геометрия,
автор: mary125
Дан треугольник АВС, угол В-прямой. Длина стороны АС равна 13, соsC=12/13. Найдите АВ.
Ответ: 5, нужно решение!
Ответы
Автор ответа:
0
I способ.
cos∠C = BC : AC
BC = AC · cos∠C = 13 · 12/13 = 12
По теореме Пифагора
АВ = √(АС² - ВС²) = √(169 - 144) = √25 = 5
II способ.
sin²∠C + cos²∠C = 1 основное тригонометрическое тождество
sin²∠C = 1 - cos²∠C = 1 - (12/13)² = 1 - 144/169 = 25/169
sin∠C = √(25/169) = 5/13
sin∠C = AB : AC
AB = AC · sin∠C = 13 · 5/13 = 5
cos∠C = BC : AC
BC = AC · cos∠C = 13 · 12/13 = 12
По теореме Пифагора
АВ = √(АС² - ВС²) = √(169 - 144) = √25 = 5
II способ.
sin²∠C + cos²∠C = 1 основное тригонометрическое тождество
sin²∠C = 1 - cos²∠C = 1 - (12/13)² = 1 - 144/169 = 25/169
sin∠C = √(25/169) = 5/13
sin∠C = AB : AC
AB = AC · sin∠C = 13 · 5/13 = 5
Приложения:
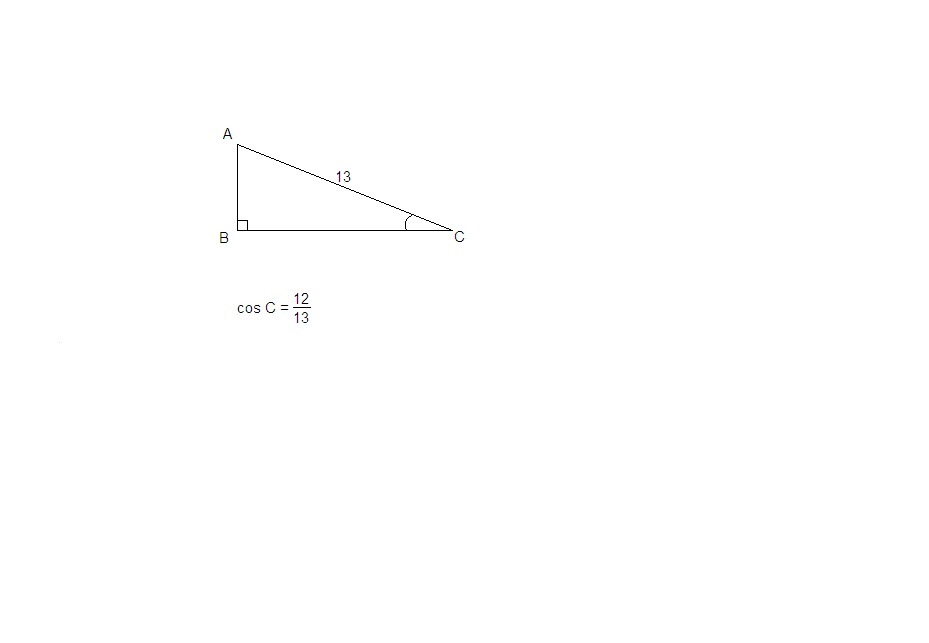
Похожие вопросы
Предмет: Қазақ тiлi,
автор: LonelY111Y
Предмет: Русский язык,
автор: ShpitserElizaveta
Предмет: Математика,
автор: afigettima
Предмет: Физика,
автор: donmalboro10049
Предмет: Алгебра,
автор: текилаша