Предмет: Геометрия,
автор: Аноним
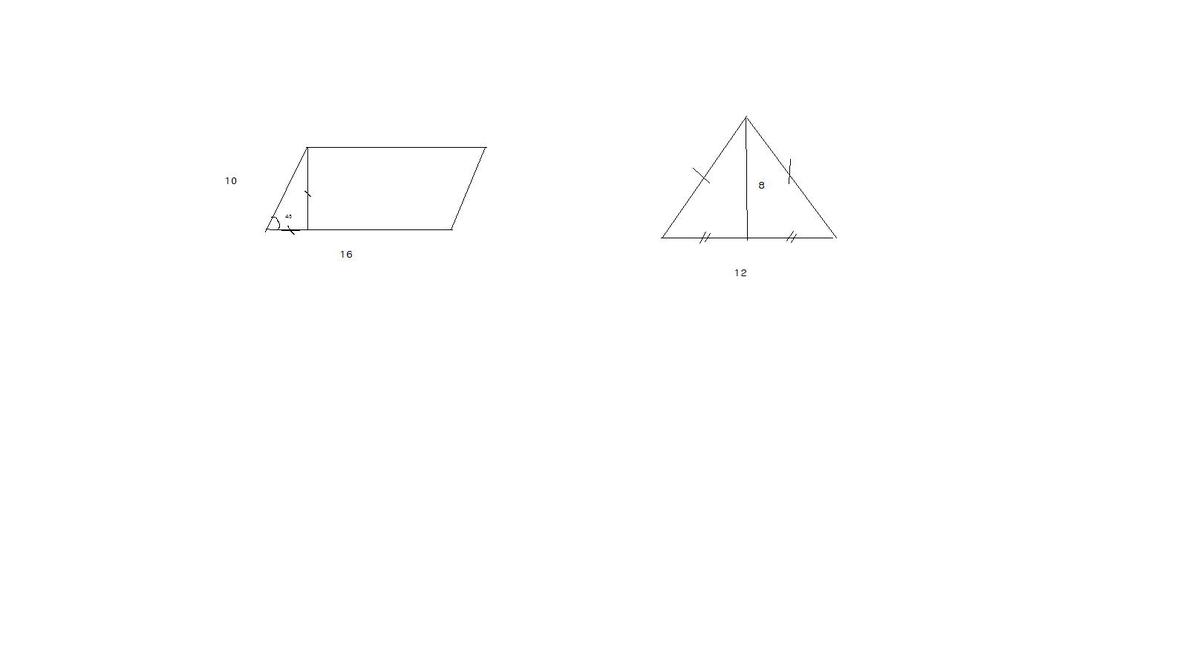
1.Найдите площадь параллелограмма, стороны которого образуют угол 45 и равны 10 см и 16 см.
2.Основа равнобедренного треугольника равна 12 см., А высота, проведенная к ней, 8 см. Найдите боковую сторону треугольника, если высота, проведенная к ней, равна 6 см.
Ответы
Автор ответа:
0
1.Решение:
Площадь можно найти по формуле S=a*b*sinα (где a-одна сторона,b-другая сторона, sinα - угол между двумя этими сторонами),получаем, S=10*16*√2/2=80√2 (см²)
Ответ: 80√2 cм²
2.Решение:
Я предположу что высота все таки равна 8.
Рисунок прикреплен ниже.
1)Если треугольник равнобедренный и к основанию проведена высота BD,то она делит основание пополам,значит AD=DC=6см 2)Рассмотрим тр ABD (угол D=90°) значит он прямоугольный.По теореме Пифагора AB=√BD²+√AD²=√36+√64=√100=10см .Значит боковая сторона равно 10см
Ответ 10 см
Площадь можно найти по формуле S=a*b*sinα (где a-одна сторона,b-другая сторона, sinα - угол между двумя этими сторонами),получаем, S=10*16*√2/2=80√2 (см²)
Ответ: 80√2 cм²
2.Решение:
Я предположу что высота все таки равна 8.
Рисунок прикреплен ниже.
1)Если треугольник равнобедренный и к основанию проведена высота BD,то она делит основание пополам,значит AD=DC=6см 2)Рассмотрим тр ABD (угол D=90°) значит он прямоугольный.По теореме Пифагора AB=√BD²+√AD²=√36+√64=√100=10см .Значит боковая сторона равно 10см
Ответ 10 см
Приложения:
Автор ответа:
0
Спасибо , но я хотел для 8 класса , мы еще Пифагора и синусы не изучали
Автор ответа:
0
1) S параллелограмма = основание * высота. Основание есть, надо найти высоту. Проводим её. Получаем прямоугольный треугольник. Один из его углов = 45° => треугольник равнобедренный. Применяем теорему Пифагора. Высота = 5√2
5√2 * 16 = 80√2 см²
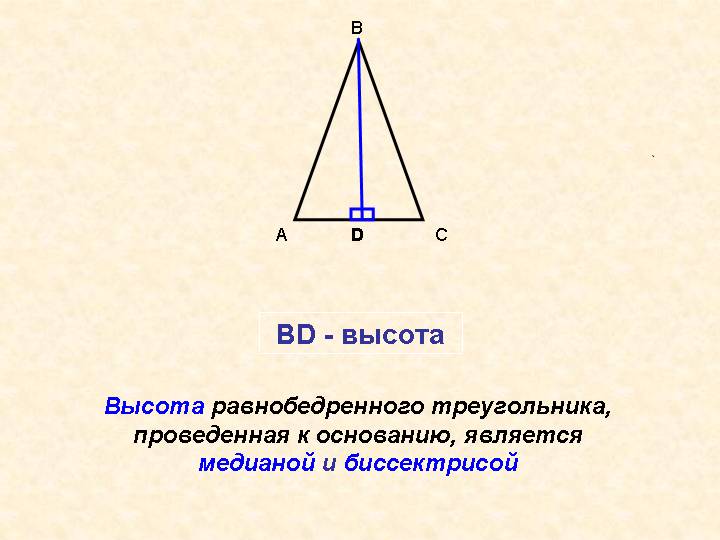
2) Высота в равнобедренном треугольнике является и медианой (линией, проходящей из вершины к середине противоположной стороны) и биссектрисой. Получаем два прямоугольных треугольника. Вычисляем по теореме Пифагора.
5√2 * 16 = 80√2 см²
2) Высота в равнобедренном треугольнике является и медианой (линией, проходящей из вершины к середине противоположной стороны) и биссектрисой. Получаем два прямоугольных треугольника. Вычисляем по теореме Пифагора.
Приложения:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: Аноним
Предмет: Английский язык,
автор: karinadavydova1014
Предмет: Математика,
автор: halloedi
Предмет: Алгебра,
автор: CoCaCola98
Предмет: Математика,
автор: Irinaaa5