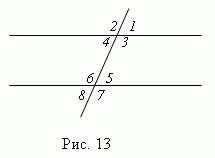Задача.В треугольнике АВС угол А равен 40 грудусам,ф угол ВСЕ смежный с углом АСВ,равен 80 градусам.Докажите что биссектриса угла ВСЕ параллельны прямой АВ.Пожалусто полное решение а то непонял эту тему(((((((
Ответы
Угол BCA бцдет равен 100 градусам, тк он смежный с углом BCE (180-80=100)
угол ABC = 180-100-40=40 градусов.
Биссектрисса(СD) делит угол BCE пополам => 2 угла по 40 градусов.
AB параллельна CD, потому что угол BCD= углуBAC (эти углы накрест лежащие)
«Параллельные прямые 7 класс»
Переписывать все то, что можно с успехом прочитать в учебнике, чтобы разобраться в непонятной теме - дело совершенно лишнее.
--------------------------------------------------
Коротко:
При пересечении двух параллельных прямых третьей прямой, образуются восемь углов ( рис.13 ), которые попарно называются:
1) соответственные углы ( 1 и 5; 2 и 6; 3 и 7; 4 и 8 ); эти углы попарно
равны: ( ∠1 = ∠5; ∠2 =∠ 6; ∠3 = ∠7; ∠4 = ∠8 );
2) внутренние накрест лежащие углы ( 4 и 5; 3 и 6 ); они попарно равны;
3) внешние накрест лежащие углы ( 1 и 8; 2 и 7 ); они попарно равны;
4) внутренние односторонние углы ( 3 и 5; 4 и 6 ); их сумма равна 180°
---------------------------------
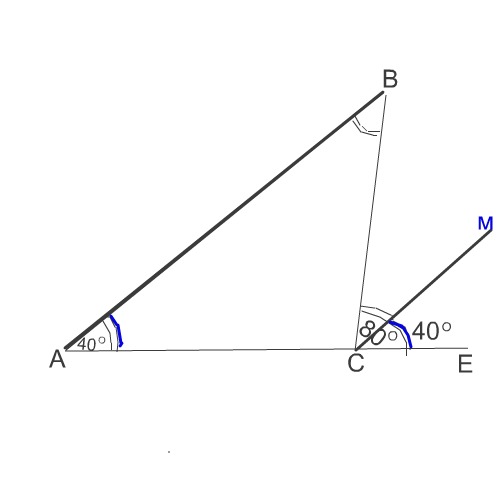
Смотрим рисунок к задаче:
∠АВС =∠ МСЕ,
один равен 40° по условию задачи, второй - по построению ( СМ - биссектриса и делит ∠ 80° пополам).
В данной задаче АЕ - секущая между прямыми АВ и СМ.
Соответственные ∠ВАС и ∠ МСЕ равны 40°.
Если две параллельные прямые пересечены секущей и соответственные углы равны, то эти прямые параллельны.
---------
Накрестлежащие ∠ АВС и ∠ ВСМ тоже равны, т.к.∠АСВ, как смежный ∠ВСЕ= 80° равен 100°, следовательно, из суммы углов треугольника следует, что угол ∠ АВС=40°.