Question

Сделайте добренькое дело решите задачку ))
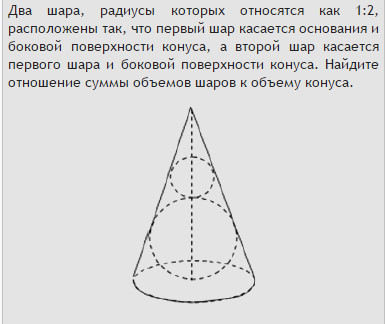
Два шара, радиусы которых относятся как 1:2, расположены так, что первый шар касается основания и боковой поверхности конуса, а второй шар касается первого шара и боковой поверхности конуса. Найдите отношение суммы объемов шаров к объему конуса.

Answer 1

Если x - расстояние от центра верхнего шара до вершины конуса, а r - радиус меньшего шара, то из подобия треугольников (x+3r)/x=2r/r, откуда x=3r. Если a - угол между высотой конуса и его образующей, то sin(a)=r/(3r)=1/3. Значит tg(a)=$frac{1}{2sqrt{2}}$. Поэтому радиус основания R=8r*tg(a)=$2sqrt{2}r$, т.к. высота конуса равна 8r. Значит объем конуса равен (8r*pi*8r^2)/3=(64Pi*r^3)/3. Объем шаров равен 4Pi/3*(r^3+8r^3)=12Pi*r^3. Отсюда искомое отношение равно 9/16.

Answer 2

упс, немного ошибся с объемом конуса. Сейчас поправлю.