Question

Помогите решить эту задачу

Условие такое: дана трапеция и в неё вписана окружность. Надо найти расстояние между точками касания боковых сторон если основания раны 6 и 14
с решением!!!!

Answer 1

В четырехугольник, значит, и в трапецию, вписать окружность можно тогда и только тогда, когда суммы ее противоположных сторон равны. 
Следовательно,
АВ+СD=AD+BC=20
В комментарии к условию указано, что трапеция равнобедренная. Следовательно.
АВ=СD=20:2=10 
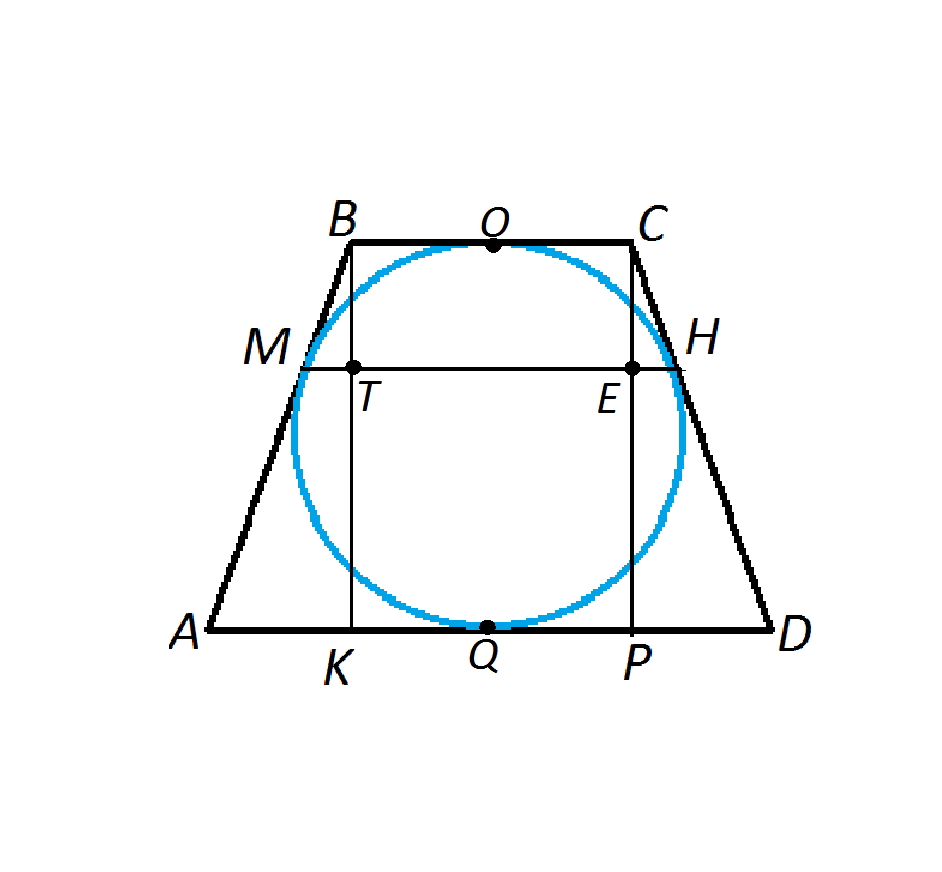
Соединим точки касания окружности М и Н. 
Опустим из В и С перпендикуляры ВК и СР. 
КР=ВС=ТЕ=6 
АК=(АD-DC):2=(14-6):2=4 
По свойству отрезков касательной из одной точки 
ВМ=ВО=ОС=СН=3 
Тогда АМ=НD=10-3=7 
Рассмотрим треугольники АВК и ВМТ.
Они подобны, т.к. МН параллельна АD⇒. 
МТ:АК=ВМ:ВА 
МТ:4=3:10 
10 МТ=12 
МТ=1,2 
ЕН=МТ 
МН=МТ+ТЕ+ЕН=8,6

Answer 2

Spasibo za obyasnenie! Realno pomoqli)