Question

в трапеции длина одной из диагоналей равна сумме длин оснований, а угол между диагоналями равен 60°.Докажите, что трапеция-равнобедренная.
ПОМОГИТЕ ПРОШУ ВАС!!!!!! на вас вся надежда((((((

Answer 1

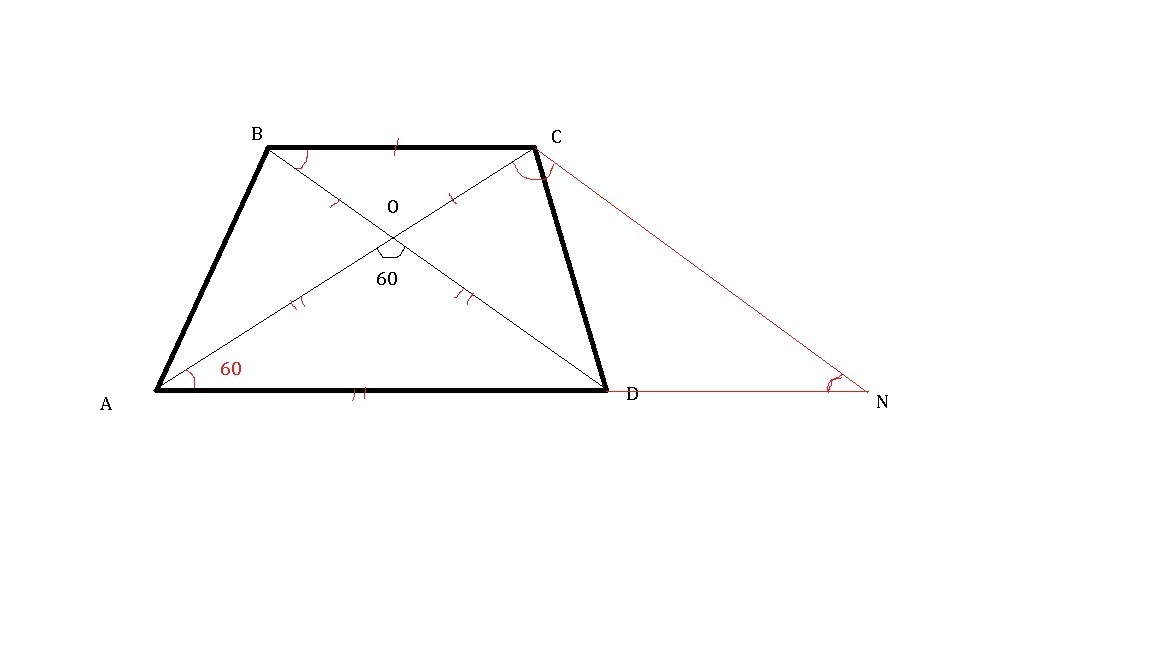
Нарисуем трапецию ABCD, где AD и ВС основания трапеции.
Продолжим сторону AD  до точки N, где  DN=BC.
Рассмотрим получившийся треугольник ΔACN.
АС= AD + ВС  по условию
AN=AD+DN=AD+BC=AC, следовательно ΔACN - равнобедренный
BCDN - параллелограмм (BC+DN, BC║DN) ⇒ OD║CN ⇒ ∠AOD =∠ACN=∠CNA=60°
A значит треугольник ΔAOD - равносторонний (2 угла по 60°)
ΔBOC равносторонний (по трем углам 60°)
Отсюда диагонали BD=AC.
Следовательно  ΔCOD = ΔBOA (AO=OD, OB=OC, ∠BOA=∠COD)
⇒AB=CD ⇒ трапеция равнобедренная
Ч.т.д.