Предмет: Информатика,
автор: HeartBeat1
Помогите решить уравнение по информатике
Приложения:
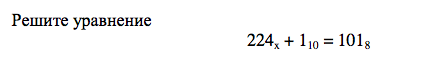
Ответы
Автор ответа:
0
Сначала переведем число 101 из восьмеричной системы счисления в десятичную. Получим 65.
Теперь мы знаем, что число в десятичной системе должно быть равно 64 (чтобы выполнялось равенство). Поэтому просто берем и переводим 64 в другие системы счисления. Сразу пропускаем двоичную, троичную и четверичную, потому что числа 224 в этих системах счисления не существует. А вот в пятеричной как раз
в десятичной системе должно быть равно 64 (чтобы выполнялось равенство). Поэтому просто берем и переводим 64 в другие системы счисления. Сразу пропускаем двоичную, троичную и четверичную, потому что числа 224 в этих системах счисления не существует. А вот в пятеричной как раз 
Ответ: х = 5
Теперь мы знаем, что число
Ответ: х = 5
Автор ответа:
0
Очевидно, что отрицательное х нам не подходит, поэтому остается решение х=5.
Ответ: х=5 (система счисления пятеричная).
Похожие вопросы
Предмет: Биология,
автор: tehon1003
Предмет: Литература,
автор: ivankarhanin01
Предмет: Математика,
автор: lebedeva2003al
Предмет: Литература,
автор: AlsuYarullina00Хоран
Предмет: Обществознание,
автор: Oksana1969bk