Предмет: Геометрия,
автор: ABC1234567
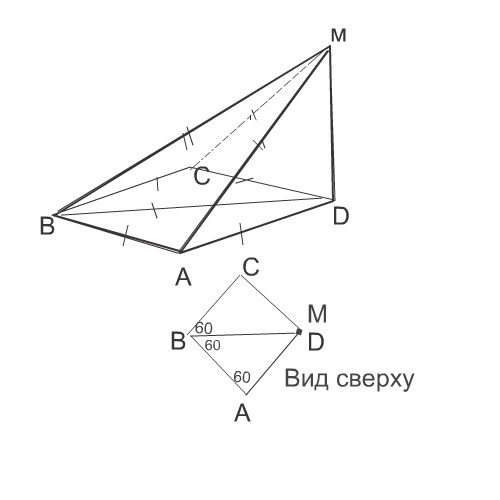
Точка М выбрана вне плоскости ромба ABCD так, что отрезки АМ, ВМ и СМ равны, а отрезок МD перпендикулярен плоскости АВС. Найдите углы ромба.
Ответы
Автор ответа:
0
При соединении точки М и вершин при углах ромба получаем пирамиду, три стороны которой соединены в точке М и равны. МD - перпендикуляр, АМ, ВМ и СМ равные наклонные, и проекции их, естественно, тоже равны. Отсюда диагональ ромба ВD равна сторонам ромба.
Вывод: ромб составлен из 2-х равносторонних треугольников.
Острые углы в нем равны 60°,
тупые 60·2=120°
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: nuraimkas
Предмет: Математика,
автор: stoyanovakate1
Предмет: Математика,
автор: sakinatolipova
Предмет: Физика,
автор: grooveone
Предмет: Алгебра,
автор: manjek