Предмет: Алгебра,
автор: abcdefg321
Помогите решить , пожалуйста, логорифм !!
Приложения:
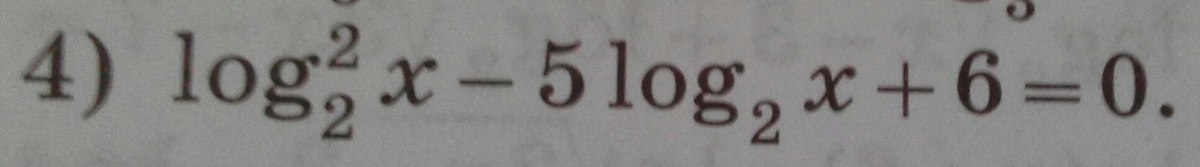
Ответы
Автор ответа:
0
Пусть
по т. Виета
Возвращаемся к замене
Автор ответа:
0
по Теореме Виетта
тогда мы имеем
Похожие вопросы
Предмет: Русский язык,
автор: panidaesrkepova
Предмет: Алгебра,
автор: Аноним
Предмет: Английский язык,
автор: iliashishki
Предмет: Литература,
автор: orehgalya
Предмет: География,
автор: NiceSweet