Предмет: Алгебра,
автор: tampi43
Всех приветствую! Прошу помочь с уравнениями:
Приложения:
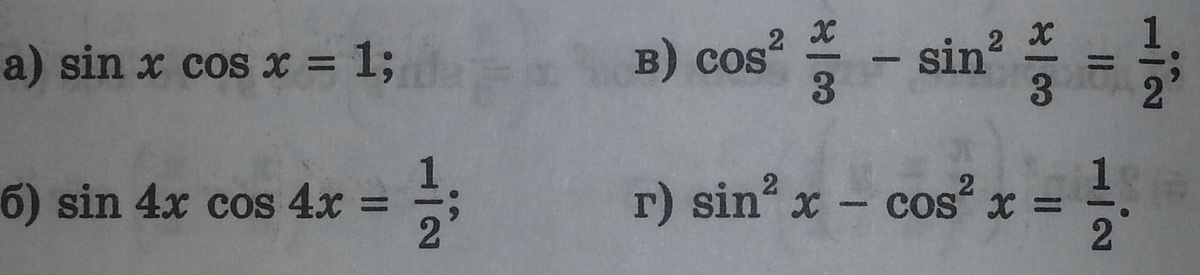
Ответы
Автор ответа:
0
1) sinxcosx = 1 умножим обе части уравнения на 2
2sinxcosx = 2
sin2x = 2
уравнение решений не имеет, так как не условию: IsinxI ≤ 1
2) sin4xcos4x = 1/2 умножим обе части уравнения на 2
2sin4xcos4x = 1
sin8x = 1
8x = π/2 + 2πk, k∈Z
x = π/16 + πk/4, k∈Z
3) cos²(x/3) - sin²(x/3) = 1/2
cos(2x/3) = 1/2
2x/3 = (+ -)arccos(1/2) + 2πn, n∈Z
2x/3 = (+ -) (π/3) + 2πn, n∈Z
x = (+ -) (π/2) + 3πn, n∈Z
4) sin²x - cos²x = 1/2
cos2x = - 1/2
2x = (+ -) arccos(-1/2) + 2πn, n∈Z
2x = (+ -) (π - arccos(1/2)) + 2πn, n∈Z
2x = (+ -) (π - π/3) + 2πn, n∈Z
2x = (+ -) (2π/3) + 2πn, n∈Z
x = (+ -) (π/3) + πn, n∈Z
2sinxcosx = 2
sin2x = 2
уравнение решений не имеет, так как не условию: IsinxI ≤ 1
2) sin4xcos4x = 1/2 умножим обе части уравнения на 2
2sin4xcos4x = 1
sin8x = 1
8x = π/2 + 2πk, k∈Z
x = π/16 + πk/4, k∈Z
3) cos²(x/3) - sin²(x/3) = 1/2
cos(2x/3) = 1/2
2x/3 = (+ -)arccos(1/2) + 2πn, n∈Z
2x/3 = (+ -) (π/3) + 2πn, n∈Z
x = (+ -) (π/2) + 3πn, n∈Z
4) sin²x - cos²x = 1/2
cos2x = - 1/2
2x = (+ -) arccos(-1/2) + 2πn, n∈Z
2x = (+ -) (π - arccos(1/2)) + 2πn, n∈Z
2x = (+ -) (π - π/3) + 2πn, n∈Z
2x = (+ -) (2π/3) + 2πn, n∈Z
x = (+ -) (π/3) + πn, n∈Z
Похожие вопросы
Предмет: Беларуская мова,
автор: karinafedotova345
Предмет: Литература,
автор: Аноним
Предмет: Қазақ тiлi,
автор: standoff117
Предмет: Физика,
автор: NinaCarolina