Question

1) решите уравнение sin2x + 2sin^2x =0
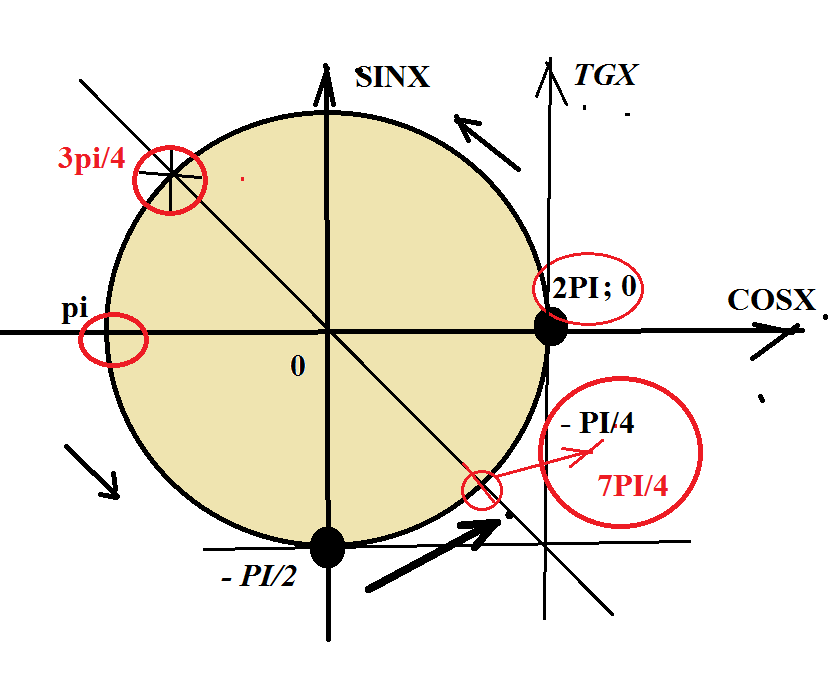
2) найдите все корни этого уравнения ,принадлежащие отрезку(2п;-п/2)
Пожалуйста с подробностями и очень четко и точно,если кого-нибудь не затруднит ,то от руки напишите,но буду рада и электронному ответу.

Answer 1

sin2x  + 2sin^2x = 0 
2sinxcosx + 2sin^2x = 0 
sinxcosx + sin^2x = 0 
sinx (cosx + sinx) = 0 

1) sinx = 0 
x = pik, k ∈ Z

2)
sinx + cosx = 0   // : cosx≠0
tgx + 1 = 0 
tgx = - 1 
x = arctg ( - 1)  + pik
x = - pi/4 + pik, k ∈ Z
 
+  ОТБОР 
-----------------------------------------

Answer 2

спасибо большое)с пи уравнения никогда не давались...я вам завидую)))

Answer 3

обнови страницу, там отбор не о той задачи был