Предмет: Алгебра,
автор: Аноним
Решите неравенство :

Ответы
Автор ответа:
0
Переносим все в левую часть:
(x-7) выносим за скобку:
Чтобы воспользоваться методом интервала находим корни многочлена, стоящего в левой части:
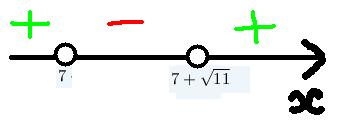
Наносим полученные корни на числовую прямую, все корни нечетной кратности, поэтому знаки будут чередоваться - картинка
Так как мы решаем неравенство <0, то в ответ попадает интервал со знаком "-".
Ответ:
Приложения:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: Аноним
Предмет: География,
автор: Аноним
Предмет: История,
автор: sergiymelnikcom
Предмет: Математика,
автор: Аноним