Предмет: Алгебра,
автор: Kristusha00
Помогите пожалуйста решить вторую часть
Приложения:
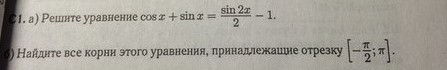
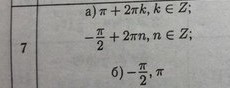
Ответы
Автор ответа:
0
Пусть
Возвращаемся к замене
Есть такой пример
Сделаем
Для задания б)
Автор ответа:
0
Подбор: k=-1; x=-п/2
Автор ответа:
0
Добавил и для б)
Автор ответа:
0
Обновите страницу
Автор ответа:
0
спасибо большое
Похожие вопросы
Предмет: Русский язык,
автор: memodel56
Предмет: Информатика,
автор: Аноним
Предмет: Алгебра,
автор: mayashnejder1234567
Предмет: Математика,
автор: Заргата