Предмет: Геометрия,
автор: Maliaa
Помогите,пожалуйста!
1) Найдите площадь ромба,сторона которого равна 25 см,а разность диагоналей 10 см
2) Угол между сторонами параллелограмма равен 60 градусов,одна из его сторон 8 см,а площадь = 56 см квадратных.Найдите вторую сторону.
Ответы
Автор ответа:
0
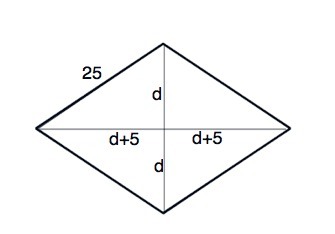
1) Диагонали ромба взаимно перпендикулярны и делят ромб на 4 равных прямоугольных треугольника. Примем половину меньшей диагонали равной d, Тогда половина большей d+5, и эти половины - катеты прямоугольного треугольника с гипотенузой 25 см.
По т.Пифагора 25²=а*+(d+5)²
625=d²+d*+10d+25=>
d²+5d-300=0
Решив квадратное уравнение, получим d=15 (второй корень отрицательный и не подходит).
Меньшая диагональ равна 2d=30 см,
Большая=30+10=40 см²
Площадь ромба равна половине произведения его диагоналей.
S=30•40:2=600 cм² ( В приложении дан рисунок ромба)
—————
2) Одна из формул площади параллелограмма
S=a•b•sinα, где а и b – стороны, α - угол между ними.
sin60°=√3/2
8•b•√3/2=56 => b=14/√3
Проверка:
S=8•14/√3•(√3/2)=56 см²
Приложения:
Похожие вопросы
Предмет: История,
автор: Аноним
Предмет: Қазақ тiлi,
автор: gajnituzelbek
Предмет: Математика,
автор: rosefox27
Предмет: Математика,
автор: наташкачер2003