Предмет: Алгебра,
автор: Аноним
Постройте график функции y = |x² - x - 12 | и определите , при каких значениях параметра а прямая у = а имеет с графиком три или более общих точек .
Ответы
Автор ответа:
0
График функции у=|f(x)| представляет собой видоизмененный график функции y=f(x): часть графика, находящаяся выше оси х, остается без изменений, а часть графика, находящаяся ниже оси х, отображается в верхнюю полуплоскость. Таким образом, весь график функции у=|f(x)| находится не ниже оси х.
Строим график функции у=x²-x-12:
Это стандартная парабола с вершиной в точке с координатами, которые мы сейчас определим:

Для контроля можно просчитать пару точек:

Рисуем график - оранжевая линия
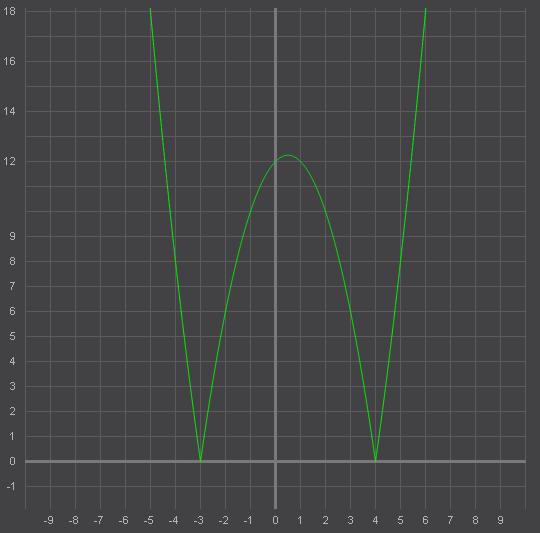
Строим график функции у=|x²-x-12|:
Часть графика у=x²-x-12 из нижней полуплоскости (при -3<x<4) отображаем в верхнюю полуплоскость. Соответственно вершина параболы будет располагаться в точке с координатами (0,5; 12,25)
Рисуем график - зеленая линия
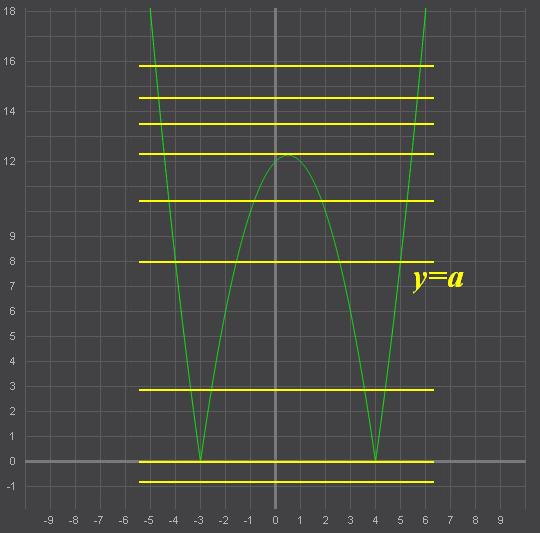
Находим значения параметра а:
Прямая у=а представляет собой прямую, параллельную оси х
- при а<0 - нет пересечений
- при а=0 - 2 пересечения
- при 0<а<12,25 - 4 пересечения
- при а=12,25 - 3 пересечения
- при а>12,25 - 2 пересечения
Ответ:![ain(0;12,25] ain(0;12,25]](https://tex.z-dn.net/?f=ain%280%3B12%2C25%5D)
Строим график функции у=x²-x-12:
Это стандартная парабола с вершиной в точке с координатами, которые мы сейчас определим:
Для контроля можно просчитать пару точек:
Рисуем график - оранжевая линия
Строим график функции у=|x²-x-12|:
Часть графика у=x²-x-12 из нижней полуплоскости (при -3<x<4) отображаем в верхнюю полуплоскость. Соответственно вершина параболы будет располагаться в точке с координатами (0,5; 12,25)
Рисуем график - зеленая линия
Находим значения параметра а:
Прямая у=а представляет собой прямую, параллельную оси х
- при а<0 - нет пересечений
- при а=0 - 2 пересечения
- при 0<а<12,25 - 4 пересечения
- при а=12,25 - 3 пересечения
- при а>12,25 - 2 пересечения
Ответ:
Приложения:

Автор ответа:
0
Спасибо.
Похожие вопросы
Предмет: Окружающий мир,
автор: Аноним
Предмет: Математика,
автор: polinakostenko663
Предмет: Математика,
автор: v9018548
Предмет: Математика,
автор: romka10376