Предмет: Математика,
автор: julialokaychuk1
помогите пожалуйста решить
Приложения:
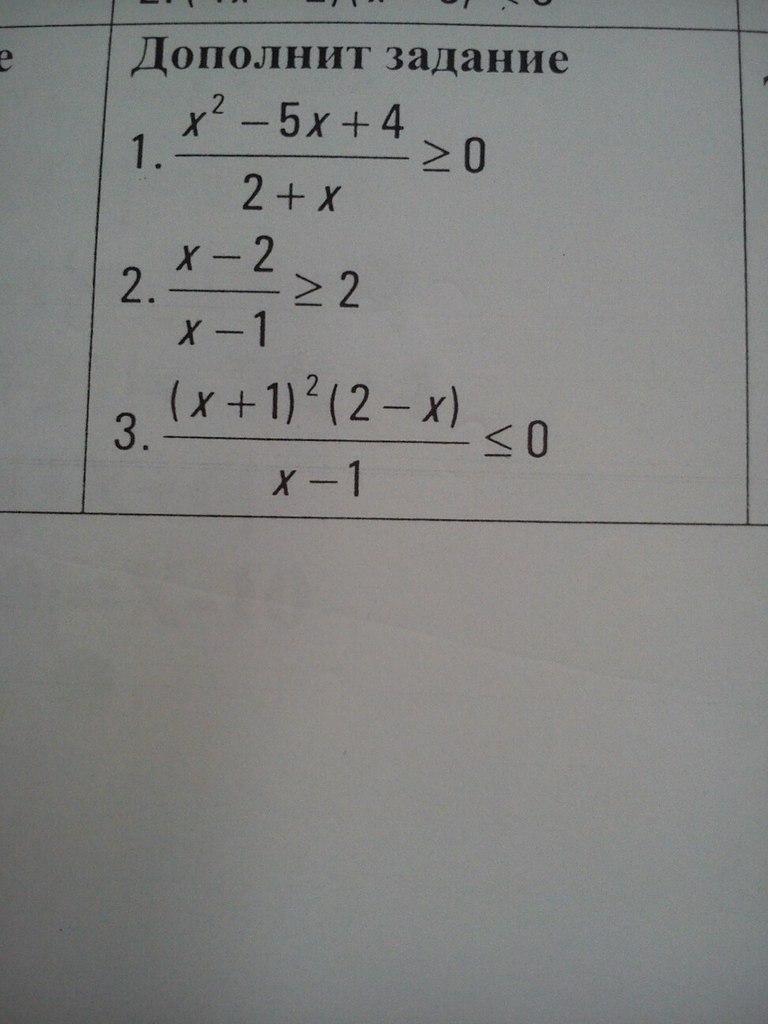
Ответы
Автор ответа:
0
1) 
разложим числитель на множители
любое квадратное уравнение можно разложить на множители по формуле: a +bx+c = a(x-
+bx+c = a(x- )(x-
)(x- ). где
). где  и
и  – корни уравнения.
– корни уравнения.
в данном случае

получаем:

далее методом интервалов получаем ответ:
x∈(-2;1]U[4;+∞)
2) переносим 2 в левую часть с противоположным знаком
переносим 2 в левую часть с противоположным знаком


Ответ: x∈[0;1)
3) тоже методом интервалов
x∈(-∞;1)U[2;+∞)
разложим числитель на множители
любое квадратное уравнение можно разложить на множители по формуле: a
в данном случае
получаем:
далее методом интервалов получаем ответ:
x∈(-2;1]U[4;+∞)
2)
Ответ: x∈[0;1)
3) тоже методом интервалов
x∈(-∞;1)U[2;+∞)
Похожие вопросы
Предмет: Другие предметы,
автор: Аноним
Предмет: Алгебра,
автор: lenanaumenko69
Предмет: Английский язык,
автор: tolendiulyaibar
Предмет: Биология,
автор: laptevatanya20
Предмет: Математика,
автор: Evgen1304