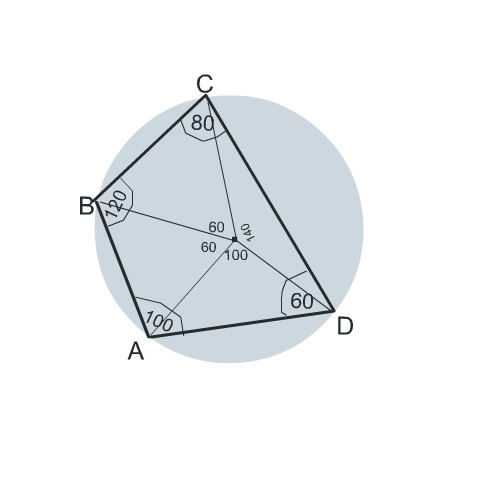
Окружность разделена точками на 4 части градусные величины которых относятся как 3:7:5:3 . Найдите углы многоугольника полученного последовательным соединением точек деления
Ответы
Величина углов четырехугольника равна половине градусной меры центральных углов, на которые опираются, как вписанные, углы этого четырехугольника.
Окружность делится на дуги, отношение которых 3:7:5:3, и коэффициент этого отношения равен (3+7+5+3)=18
360:18=20ᵒ.
Получившиеся дуги, на которые опираются центральные углы, равны соответственно:
3·20=60ᵒ
7·20=140ᵒ
5·20=100ᵒ
3·20=60ᵒ
------------
Вписанные в окружность углы равны:
∠ А опирается на дугу центрального угла ВС+СD=140+60=200ᵒ и равен 100ᵒ
∠ В опирается на дугу центрального угла CD+AD=100+140= 240ᵒ и равен 120ᵒ
∠ С - опирается на дугу центрального угла AB+AD=160ᵒ и равен 80ᵒ
∠ D - опирается на дугу центрального угла AB+BC=120ᵒ и равен 60ᵒ