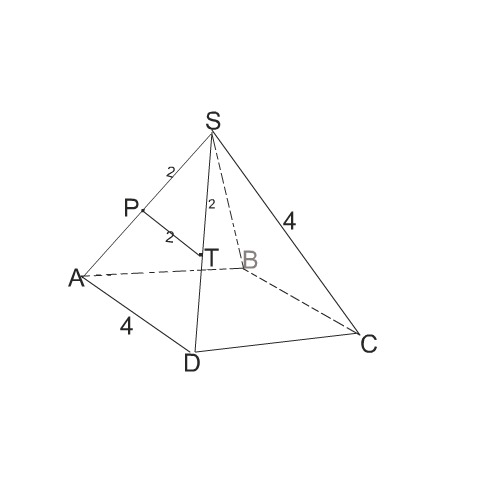
Помогите пожалуйста!:)Задача вроде бы и не трудная, но в голову ничего не лезет.)) Точки P и T - середины ребер и правильной четырехугольной пирамиды SABCD(S - вершина), длина каждого ребра кторой равна 4 сантиметра. Вычислите длину радиуса окружности, вписанной в треугольник PST.
Ответы
Для радиуса вписанной в правильный треугольник окружности есть формула:
r=√{(p-a(p-a)(p-a):p}, где r- радиус вписанной окружности, а - сторона треугольника, р - его полупериметр. После упрощения эта формула выглядит короче и легче запоминается:
r=а:(2√3), т.е радиус равен стороне, деленной на удвоенный корень из трех.
Сторона здесь - ребро грани.
Пирамида четырехугольная, в основании квадрат, а так как все ребра равны, то грани - правильные треугольники.
Стороны этого правильного треугольника равны, как дано в условии, 4 см.
Р и Т - середины сторон. Следовательно, соединив Р и Т, получим такой же правильный треугольник, только сторона в нем - 2 см.
Теперь подставим найденную сторону в формулу радиуса:
r=а:(2√3)=2:(2√3)=1:√3 или √3:3 см, что одно и то же.
Калькулятор подсказывает, что можно и так выразить:
r=0.57735026918963...