Question

Помогите,пожалуйста, решать задачу ,и если можно,то поподробней . Высота прямой призмы ABCA1B1C1 равна 4. Основание призмы - треугольник ABC , в котором AB=BC, AC=6, tgA=0,5 . Найдите тангенс угла между прямой A1B и плоскостью ACC1.

Answer 1

Высота прямой призмы АВСАВС равна 4. Основание призмы - треугольник АВС, в которомAB=BC, AC=6, tgA=0,5 . Найдите тангенс угла между прямой A₁B и плоскостью ACC₁. 
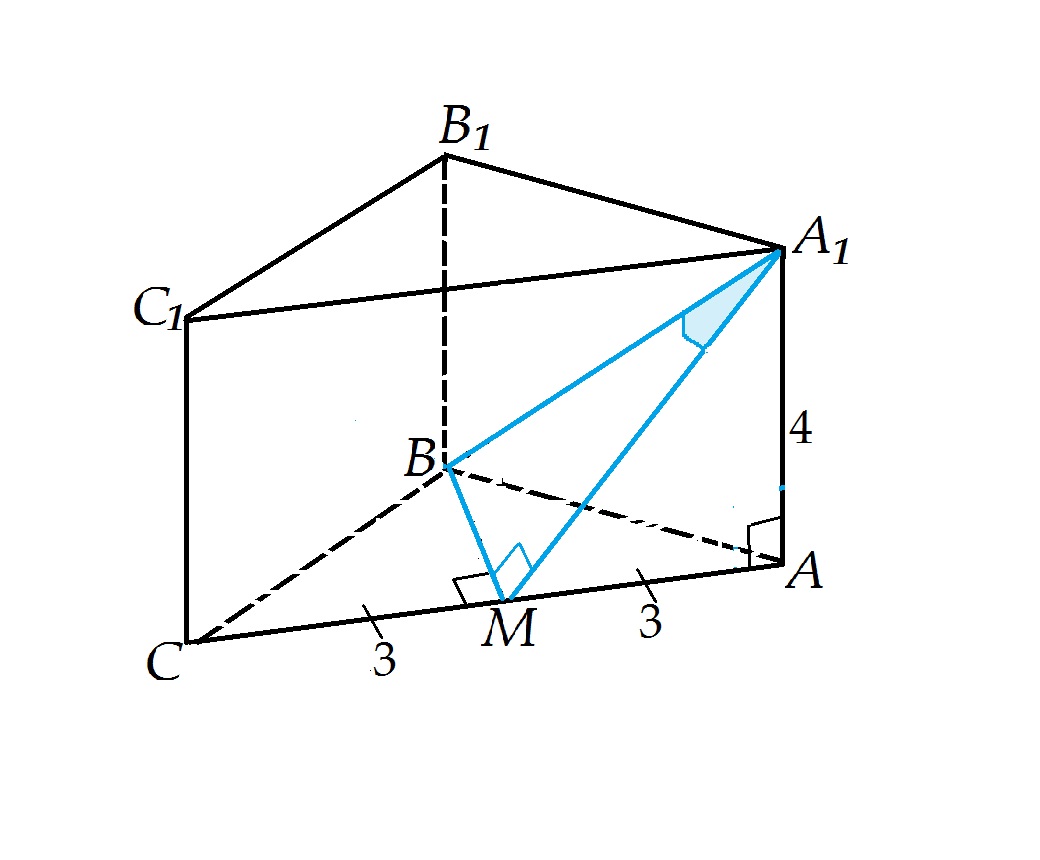
Сделаем рисунок ( см. вложение). 
Проведем в основании призмы АВС высоту ( медиану) ВМ. 
Соединим А₁ и М.
ВМ⊥АС и⊥АМ , а АМ - проекция наклонной А₁М, следовательно,
А₁М перпендикулярна ВМ по т. о трех перпендикулярах. 
Плоскость ACC₁ - это плоскость грани АСС₁А₁ 
Угол, тангенс которого нужно найти, это угол ВА₁М. 
tg ∠ ВА₁М=ВМ:А₁М. 
tg ∠А= ВМ:АМ 
СМ=АС:2=3 
ВМ=3*0,5=1,5 
В треугольнике АМА₁ катеты относятся как 3:4, следовательно он - египетский, и  МА1=5 ( можно проверить по т. Пифагора) 
tg ∠ ВА₁М=1,5:5=0,3