Предмет: Геометрия,
автор: dzirrt
Дан куб ABCDA1B1C1D1, ребро которого равно а. Секущая плоскость проходит через середину ребра AD и прямую B1C. Постройте сечение этого куба этой плоскостью и найдите его площадь
Ответы
Автор ответа:
0
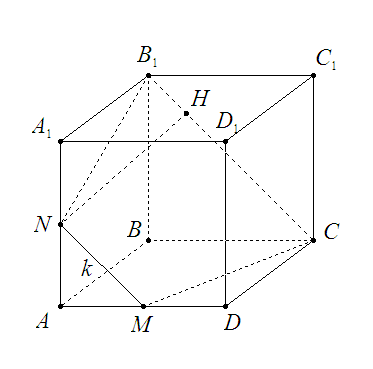
1) M - cередина AD,
M∈(ABC), C∈(ABC) ⇒ проведем MC
(B1C)∈(BCC1), M∈(ADD1), а т.к. (ADD1) || (BCC1), то секущая плоскость будет пересекать (АDD1) по прямой k, проходящей через точку М параллельно B1C. k пересечет АА1 в точке N, причем AN=NA1.
N∈(AA1B1) и B1∈(AA1B1) ⇒ проведем NB1
MNB1C - сечение куба
2) MN || B1C, CM=B1N=√(a²-(a/2)²)=a√3/2 ⇒ MNB1C трапеция
S (MNB1C) = 1/2 (MN+B1C) * NH, где NH - это высота трапеции
B1C=a√2 / 2
MN = 1/2 B1C = a√2 / 4
B1H = 1/2 (B1C - MN) = a√2 / 4
NH = √(B1N² - B1H²) = a√10 / 4
S (MNB1C) = 3 a² √5 / 16
M∈(ABC), C∈(ABC) ⇒ проведем MC
(B1C)∈(BCC1), M∈(ADD1), а т.к. (ADD1) || (BCC1), то секущая плоскость будет пересекать (АDD1) по прямой k, проходящей через точку М параллельно B1C. k пересечет АА1 в точке N, причем AN=NA1.
N∈(AA1B1) и B1∈(AA1B1) ⇒ проведем NB1
MNB1C - сечение куба
2) MN || B1C, CM=B1N=√(a²-(a/2)²)=a√3/2 ⇒ MNB1C трапеция
S (MNB1C) = 1/2 (MN+B1C) * NH, где NH - это высота трапеции
B1C=a√2 / 2
MN = 1/2 B1C = a√2 / 4
B1H = 1/2 (B1C - MN) = a√2 / 4
NH = √(B1N² - B1H²) = a√10 / 4
S (MNB1C) = 3 a² √5 / 16
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: vaflelkabrainly
Предмет: Химия,
автор: cychvj
Предмет: История,
автор: janierikxan
Предмет: Математика,
автор: Kraminn