Question

Найдите площадь ромба периметр какого равен 120 см,а одна с диагоналей равна 36 см

Answer 1

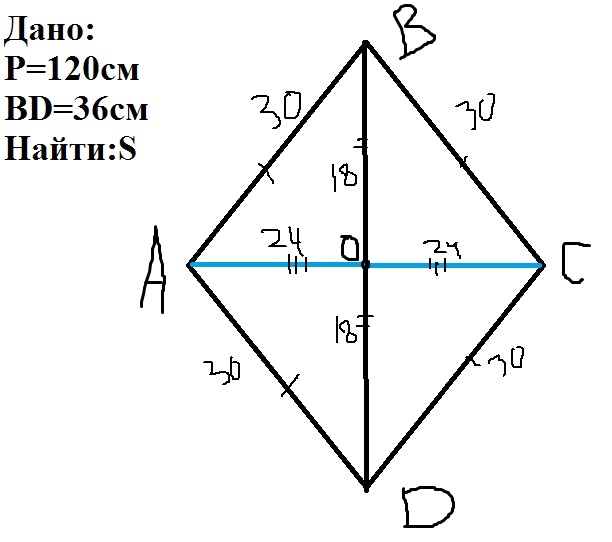
(Смотри чертеж в прикрепленном файле)
Решение:
1)У ромба все 4 стороны равны, а т.к периметр равен 120 см, то сторона ромба равна 120:4=30 см.
2)Рассмотрим треугольник АВО, он прямоугольный, т.к диагонали ромба взаимно перпендикулярны.
В ромбе диагонали точкой пересечения делятся пополам ⇒OD=OB=36:2=18 см.
По теореме Пифагора найдем АО:
AO²=AB²-OB² ⇒ AO²=900-324=576. √576=24.
АО=24см. АО=ОС.⇒ АС=24*2=48 см.
Площадь ромба равна половине произведения диагоналей. ⇒$S= frac{d1*d2}{2}$
$S= frac{36*48}{2} =864$
Ответ: 864 см²