Question

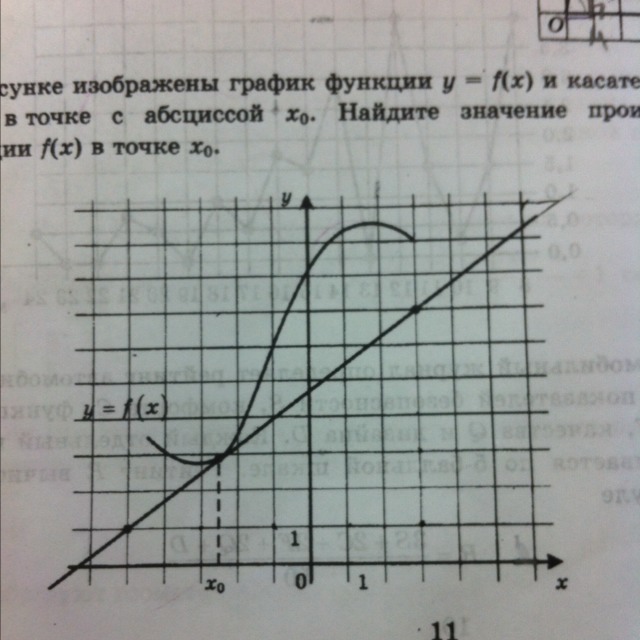
На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0

Answer 1

ищешь на графике жирные точки, они совпадают с пересечением касательной с координатной сеткой. Находишь расстояние между ними по вертикали, оно равно 6. Находишь расстояние между ними по горизонтали, оно равно 8
значение производной равно тангенсу угла наклона касательной
f'(x0) = tg a = 6/8 = 0.75

Answer 2

Значение производной в точке Х0 - это тангенс угла наклона касательной к оси ОХ,
достроив прямоугольный треугольник по точкам (-5,1) (3,1) (3,7) видим, что тангенс угла наклона  из этого треугольника  к оси ОХ (отношение противолежащей стороны к прилежащей)= 6/8 = 3/4