Предмет: Алгебра,
автор: Анна222
√18 cos^2 7п/8 - √18sin^2 7п/8 помогите решить! Очень нужно.
Приложения:
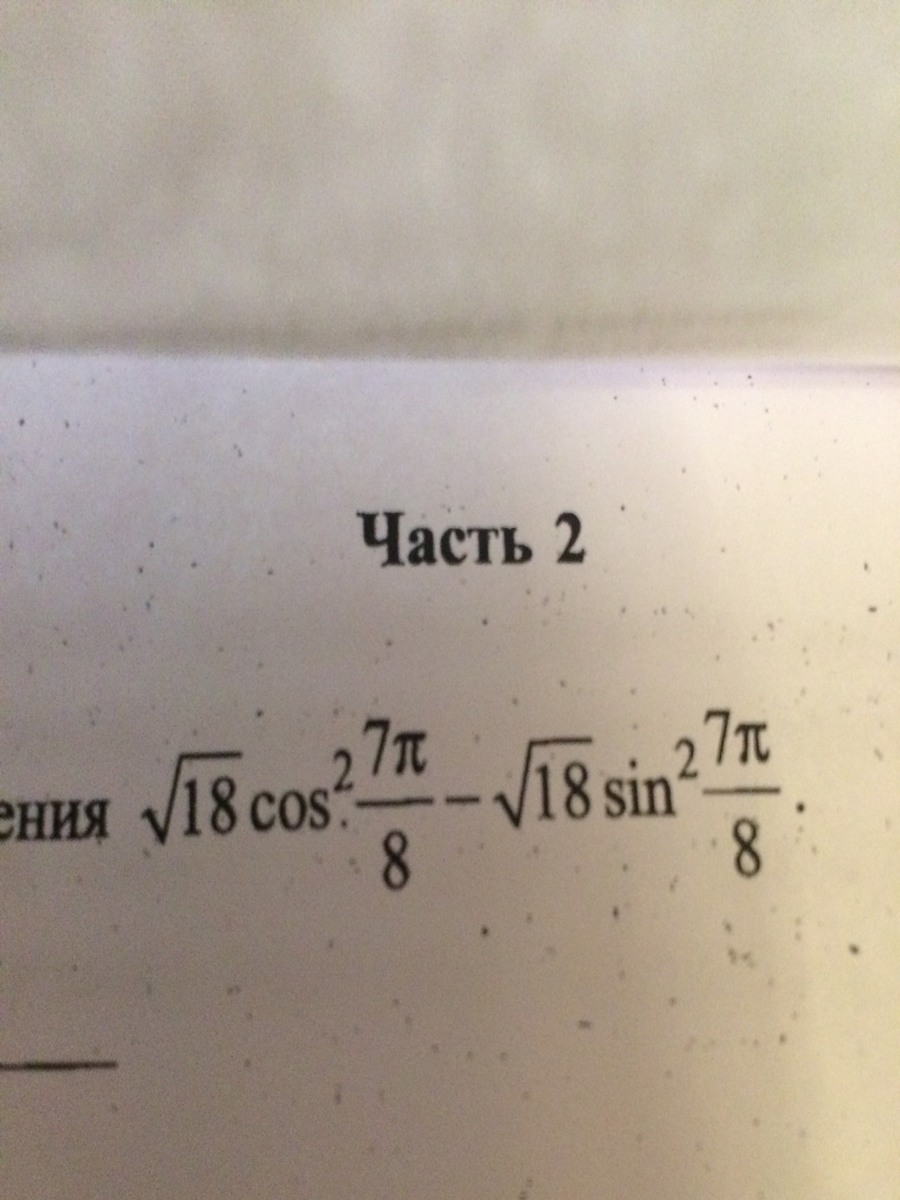
Ответы
Автор ответа:
0
√18 выносим за скобки, в скобках остается косинус двойного угла
√18*(cos^2 (7pi/8) - sin^2 (7pi/8)) = √18*cos (7pi/4) =
= √18*cos (2pi - 7pi/4) = √18*cos (pi/4) = √18*√2/2 = 3√2*√2/2 = 3
√18*(cos^2 (7pi/8) - sin^2 (7pi/8)) = √18*cos (7pi/4) =
= √18*cos (2pi - 7pi/4) = √18*cos (pi/4) = √18*√2/2 = 3√2*√2/2 = 3
Автор ответа:
0
спасибо!
Автор ответа:
0
√18(сos²7π/8-sin²7π/8)=√18cos7π/4=√18cos(2π-π/4)=√18cosπ/4=√18*√2/2=
=√36/2=6/2=3
=√36/2=6/2=3
Похожие вопросы
Предмет: Английский язык,
автор: esmanartur
Предмет: Алгебра,
автор: Wiskasssssss
Предмет: Право,
автор: madinae457
Предмет: Математика,
автор: IrShOd
Предмет: Математика,
автор: milaskaelya