Предмет: Геометрия,
автор: AlexS49
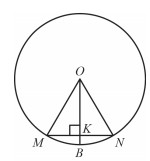
радиус OB окружности с центром в точке О пересекает хорду MN в ее середине - точке К. Найдите длину хорды MN, если КВ=1см, а радиус окружности равен 13см.
Приложения:
Ответы
Автор ответа:
0
Есть такая теоремка: диаметр, перпендикулярный хорде, делит ее пополам. В нашем случае радиус делит хорду пополам, а значит, он ей перпендикулярен!
OK=OB-KB=13-1=12
В треугольнике OMК OM=13, OK=12
по теореме Пифагора
Значит, MK=5, тогда MN=2MK=10.
Ответ: 10
Автор ответа:
0
1) OB=MO=OK=13см как радиусы окружности
2) ОК =OB-KB=13-1=12
3) Рассмотрим треугольник МОК,Он прямоугольный по условию (Угол ОКМ=90 градусов, см на график)
4) MB^2=OM^2-OK^2=169-144=25
MB=5
5) Т.К. МВ=BN, то MN=5+5=10
Похожие вопросы
Предмет: Русский язык,
автор: kozganbaevakristina
Предмет: Биология,
автор: vitalikpilsikov5902
Предмет: Алгебра,
автор: Аноним
Предмет: Алгебра,
автор: Tanya05
Предмет: Математика,
автор: Аноним