Предмет: Геометрия,
автор: Ephemeral
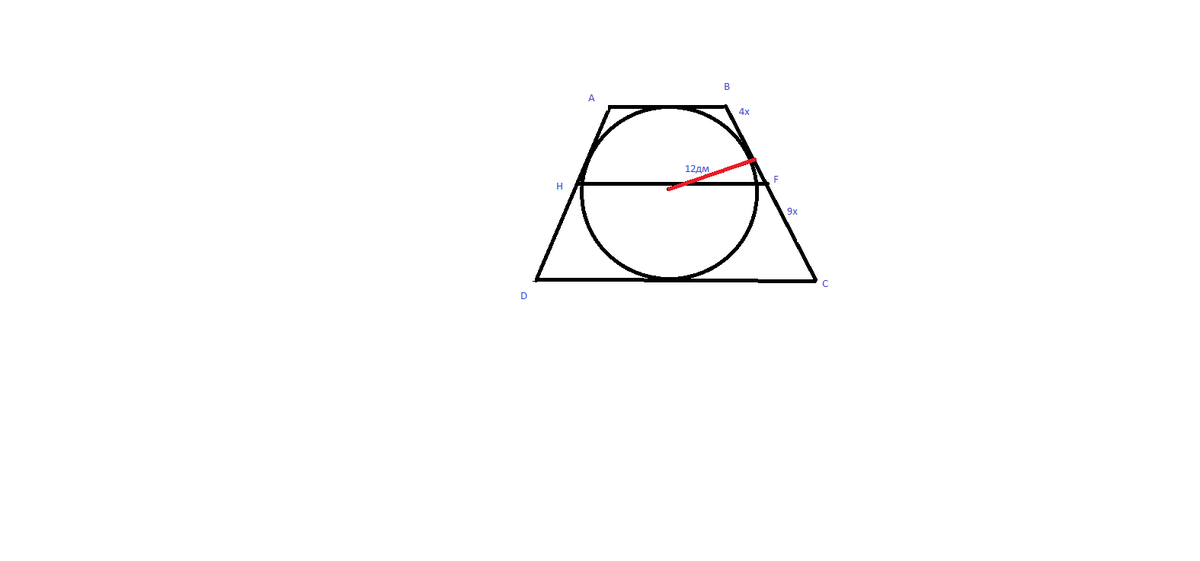
Равнобокая трапеция описана около окружности с радиусом 12 дм , точка касания делит ее боковую сторону в соотношении 9:4. Найдите среднюю линию трапеции
Ответы
Автор ответа:
0
Окр можно вписать в трапецию тогда и только тогда, когда сумма сторон
( боковых ) = сумме оснований т,е 26+26=52 ( AD+BC ) и это равно сумме оснований т,е 52 = AB+DC, 52=52
Средняя линия = полусумме оснований т,е
( ср линия )
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: milana201009
Предмет: Геометрия,
автор: aishaaktau2018
Предмет: Русский язык,
автор: ajdarerdoshan
Предмет: Биология,
автор: ali209920
Предмет: Математика,
автор: asd1967