Предмет: Геометрия,
автор: Anfanya
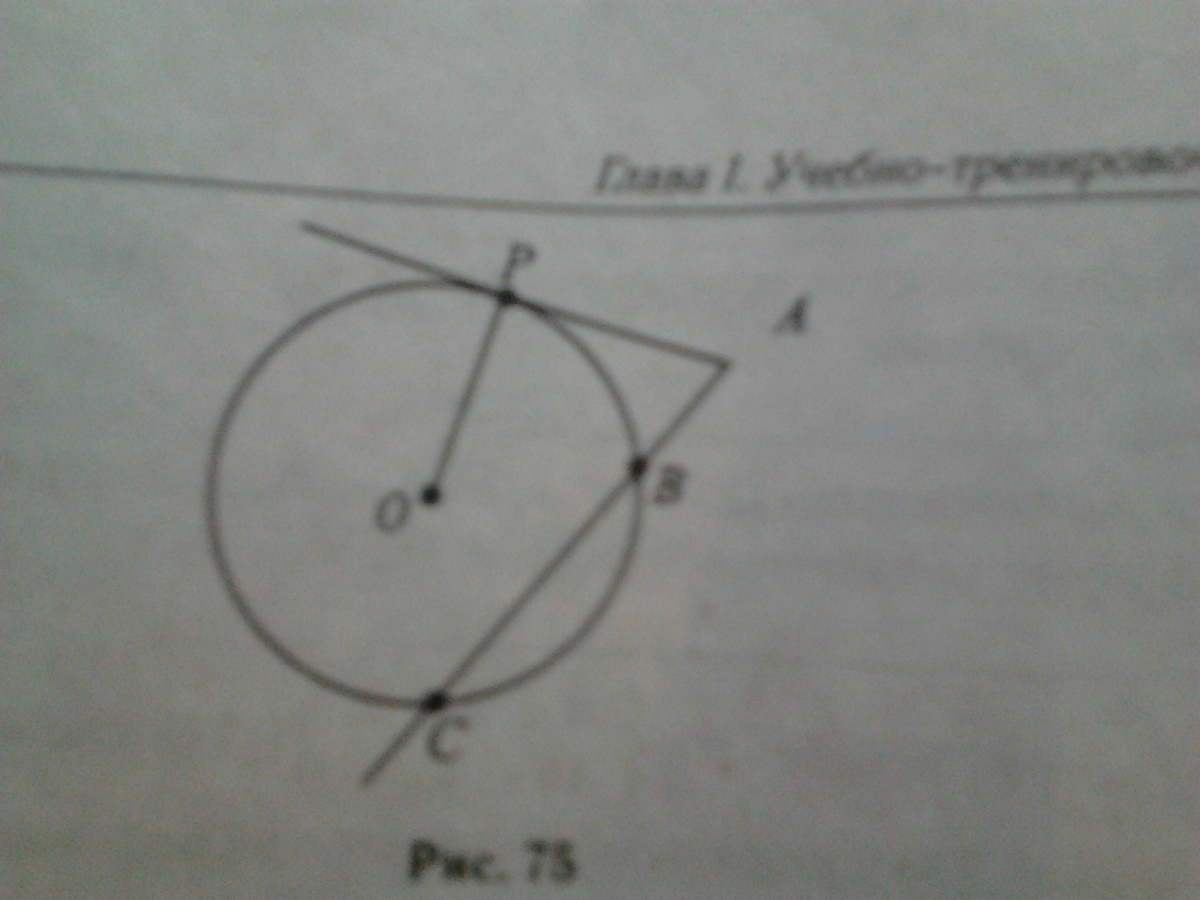
К окружности с центром в точке О проведены касательная AP и секущая АС. Найдите АР, если СВ=6см, АВ=2см.
Ответ:4, но как решить?
Приложения:
Ответы
Автор ответа:
0
есть теорема о касательной и секущей:
Если из точки, лежащей вне окружности, проведены касательная и секущая, то квадрат длины касательной равен произведению секущей на ее внешнюю часть: АР² = АВ*АС
АР² = 2*(6+2)
Если из точки, лежащей вне окружности, проведены касательная и секущая, то квадрат длины касательной равен произведению секущей на ее внешнюю часть: АР² = АВ*АС
АР² = 2*(6+2)
Похожие вопросы
Предмет: Математика,
автор: avonap0203
Предмет: Литература,
автор: korotkinaolga33
Предмет: Музыка,
автор: rxzeqqpvkvaq
Предмет: Алгебра,
автор: juliyad1999
Предмет: Обществознание,
автор: Аноним