Question

Окружности радиусов 15 и 21 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.

Answer 1

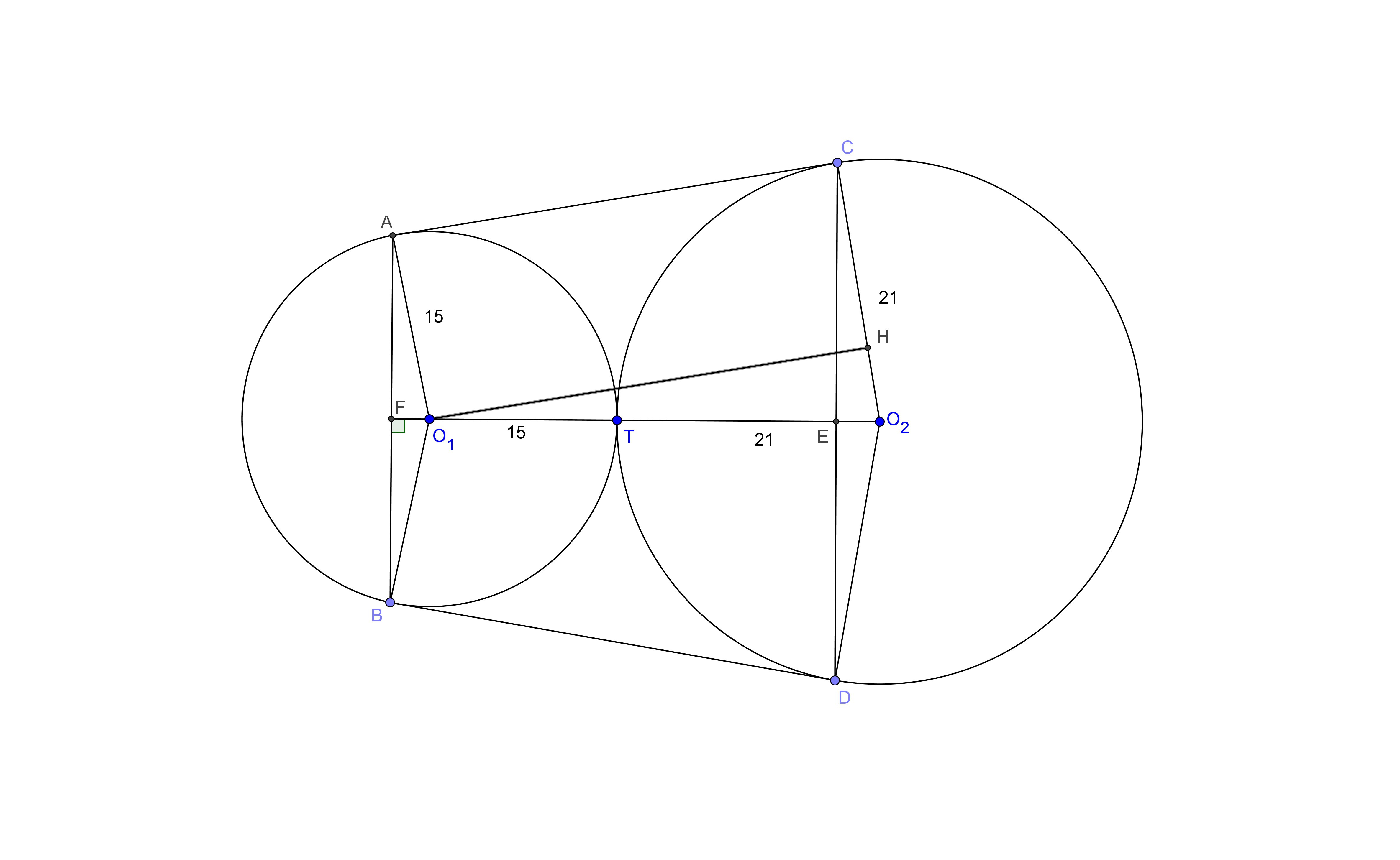
Пусть О₁ и О₂ - центры меньшей и большей окружностей соответственно, а также пусть О₁O₂ пересекает AB и CD в точках F и Е (см. рисунок). Опустим перпендикуляр O₁H на радиус O₂C. Тогда CH=AO₁=15 и
cos(∠O₁O₂H)=O₂H/O₁O₂=(21-15)/(21+15)=1/6.
Т.к. AO₁||CO₂ (они перпендикулярны AC), то ∠AO₁F=∠CO₂E=∠O₁O₂H.
Поэтому FO₁=AO₁cos(∠AO₁F)=15*1/6=5/2,
O₂E=CO₂cos(∠CO₂E)=21*1/6=7/2.
Отсюда искомое расстояние EF=FO₁+O₁O₂-O₂E=5/2+(15+21)-7/2=35.

Answer 2

Есть ли чертёж к задаче?