Question

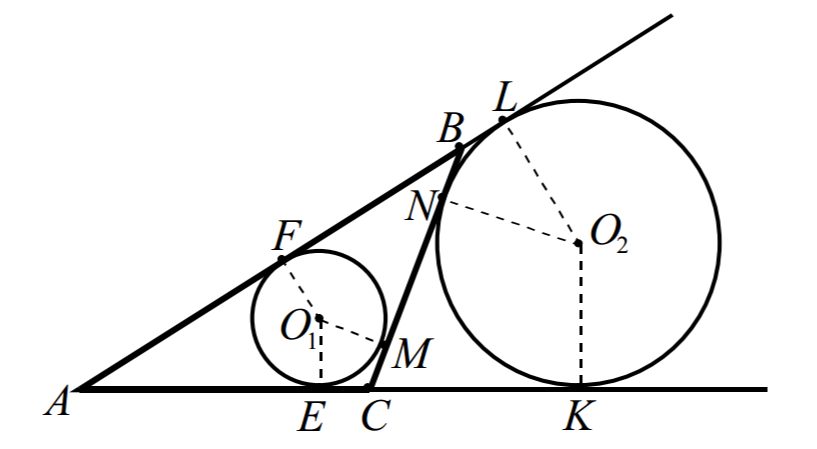
Две окружности вписаны в угол с вершиной в точке А и обе касаются отрезка BC. Как доказать, что p=AK (p - полупериметр треугольника ABC)?

Answer 1

Независимо от первой (вписанной в треугольник АВС) окружности, по свойству:
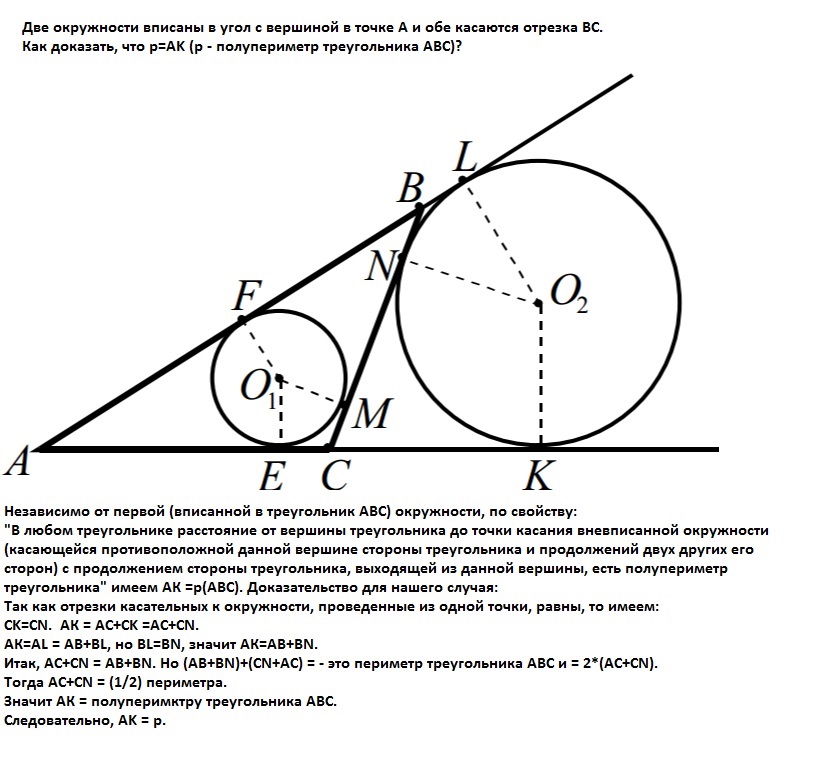
"В любом треугольнике расстояние от вершины треугольника до точки касания вневписанной окружности (касающейся противоположной данной вершине стороны треугольника и продолжений двух других его сторон) с продолжением стороны треугольника, выходящей из данной вершины, есть полупериметр треугольника"  имеем АК =р(АВС).
Доказательство для нашего случая:
Так как отрезки касательных к окружности, проведенные из одной точки, равны, то имеем:
CK=CN.  АК = АС+CK =AC+CN.
АК=AL = AB+BL, но BL=BN, значит АК=АВ+BN.
Итак, АС+CN = АВ+BN. Но (АВ+BN)+(CN+АС) = - это периметр треугольника АВС и = 2*(АС+CN).
Тогда АС+СN = (1/2) периметра. Но выше мы показали, что AC+CN = АК.
Значит АК = полуперимктру треугольника АВС, что и требовалось доказать.
Следовательно, AK = p.