Question

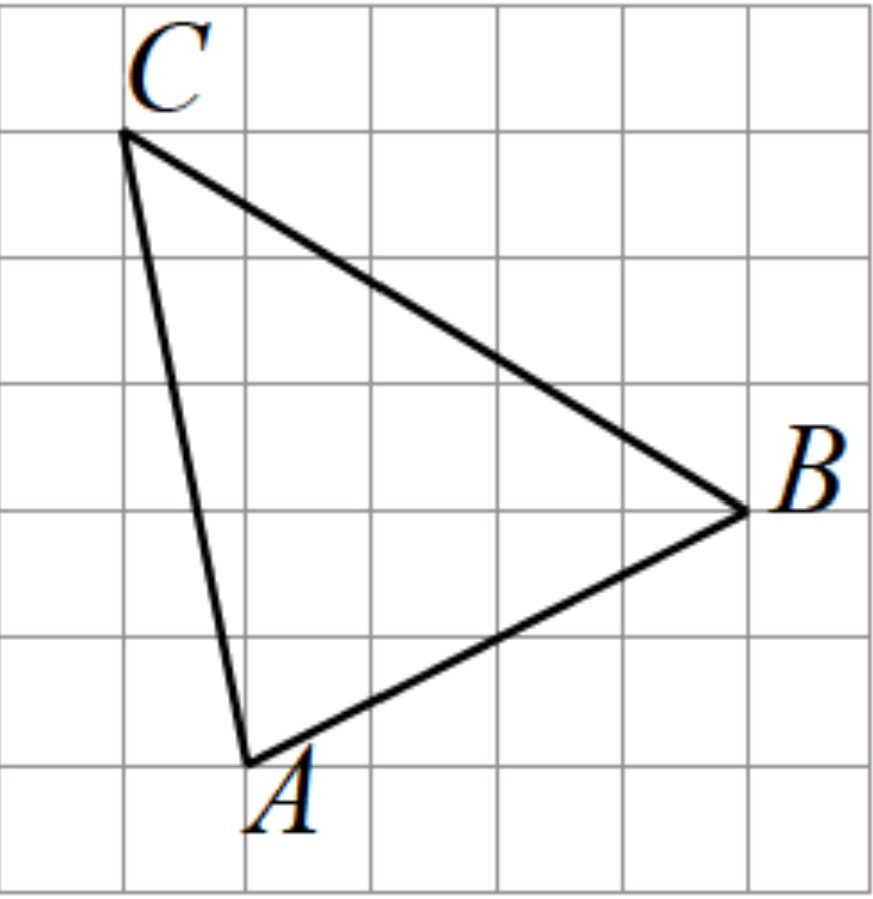
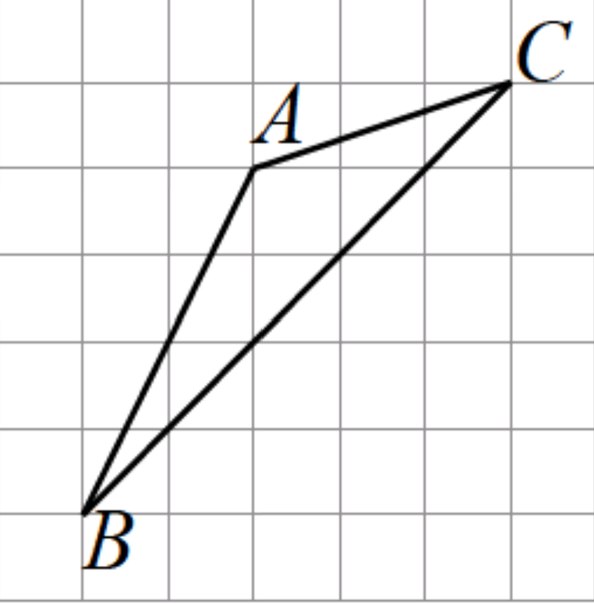
Помогите пожалуйста! Как найти медиану треугольника abc, проведенную из вершины c, если стороны квадратных клеток равны 1.

Answer 1

Формула медианы -  М = 1/2 х √ (2а² + 2b² - c²)
По теореме Пифагора находите стороны каждого треугольника по клеточкам, Вам нужны квадраты сторон.
1). а = 5² + 3² = 34;     b² = 5² + 1² = 26;    с² = 4² + 2² = 20
М  = 1/2 х √ (2 х 34 + 2 х 26 - 20) = 1/2 х √ 100 =  5
2).  а² = 5² + 5² = 25;    b² = 3² + 1² = 10;  c² = 4² + 2² = 20
М = 1/2х √ (2 х 50 + 2 х 10 - 20) = 1/2 х √ 100 = 5

Answer 2

Пардон, опечаточка. В первом случае : а квадрат = 5 квадрат + три квадрат и т.д.

Answer 3

а метод координат Вам незнаком? на первом примере построим систему координат, так что координата С будет (0;5) нетрудно заметить, что при этом координата середины АВ будет (3;1) осталось найти расстояние между точками sqrt((3-0)^2+(1-5)^2)=5 аналогично поступить и со вторым треугольником.

Answer 4

Нет проблем. Можно и так. Мне показалось эта задача для младших классов, поэтому написала доступным языкомю