Предмет: Геометрия,
автор: 0497
острый угол прямоугольного треугольника равен 32 градуса.Найдите острый угол образованный биссектрисами этого и прямого углов треугольника.
Ответы
Автор ответа:
0
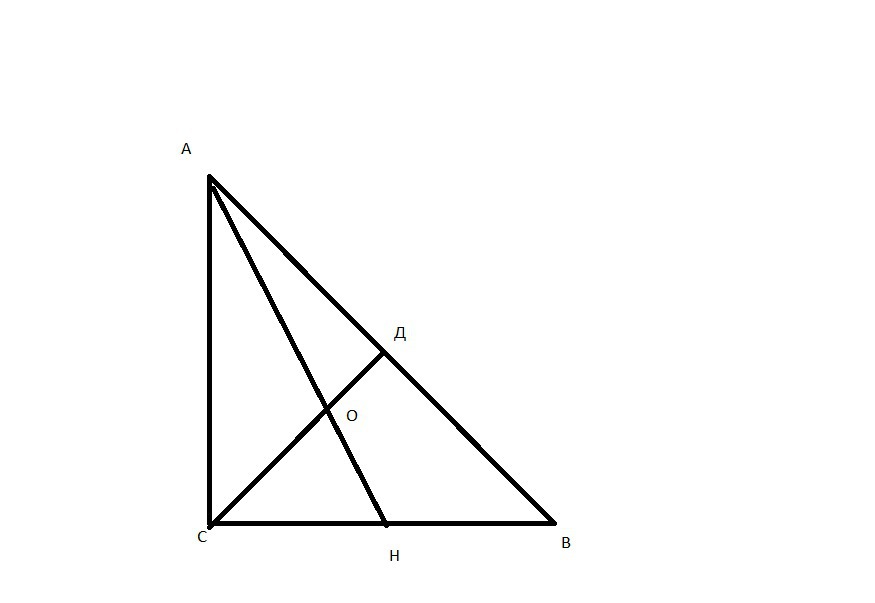
Пусть дан треугольник АВС (∠С=90*, ∠А=32*) АН, СД- биссектрисы, в точке О они пересекаются(∠САО=∠САН, ∠АСО=∠АСД,))
Биссектрисы делят углы пополам,значит:
∠САО=32/2
∠САО=16*
∠АСО=90/2
∠АСО=45*
Теперь рассмотрим треугольник АОС, мы нашли в нем два угла,поэтому сможем найти третий ∠СОА - один из образованных биссектрисами (сумма углов в треугольнике 180*)
∠СОА=180-∠САО-∠АСО
∠СОА=180-45-16
∠СОА=119 (>90*,значит,он тупой)
Рассмотрим угол ∠АОД - он смежный с ∠СОА(их сумма 180*) и тоже образован биссектрисами
∠АОД=180-∠СОА
∠АОД=180-119
∠АОД=61*(<90*,значит,он острый)
Биссектрисы делят углы пополам,значит:
∠САО=32/2
∠САО=16*
∠АСО=90/2
∠АСО=45*
Теперь рассмотрим треугольник АОС, мы нашли в нем два угла,поэтому сможем найти третий ∠СОА - один из образованных биссектрисами (сумма углов в треугольнике 180*)
∠СОА=180-∠САО-∠АСО
∠СОА=180-45-16
∠СОА=119 (>90*,значит,он тупой)
Рассмотрим угол ∠АОД - он смежный с ∠СОА(их сумма 180*) и тоже образован биссектрисами
∠АОД=180-∠СОА
∠АОД=180-119
∠АОД=61*(<90*,значит,он острый)
Приложения:
Похожие вопросы
Предмет: Математика,
автор: mashakondakova58
Предмет: Английский язык,
автор: nastyasko1
Предмет: Физика,
автор: Аноним
Предмет: Математика,
автор: ачспаро