Question

ПОМОГИТЕ ПОЖАЛУЙСТА С ЗАДАЧЕЙ, УМОЛЯЮ!


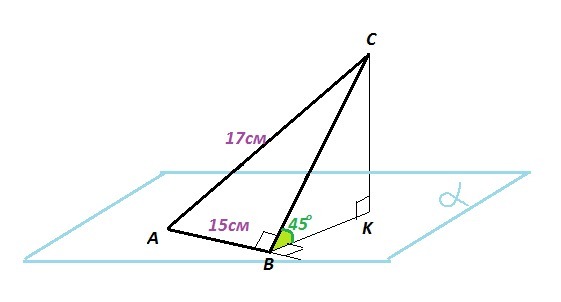
Катет АВ прямоугольного треугольника АВС (угол В=90°) лежит в плоскости а. Найдите расстояние от точки С до плоскости а, если АС=17см, АВ=15см, а двугранный угол между плоскостями АВС и а равен 45°. (С рисунком)

Answer 1

Дано:  ΔABC, ∠B=90°, AC=17 см, AB=15 см, AB∈α, ∠(ABC,α)=45°

Найти: CK - ?

Решение :

ΔABC - прямоугольный, теорема Пифагора

BC² = AC² - AB² = 17²-15² = 64 = 8²

BC = 8 см

CB⊥AB   и   CK⊥α     ⇒  по теореме о трёх перпендикулярах

KB ⊥ AB   ⇒    ∠CBK равен двугранному углу между плоскостью треугольника  ABC  и плоскостью  α    ⇒

∠CBK = 45°

ΔCBK - прямоугольный ⇒ ∠BCK=90°- ∠CBK = 90°-45° = 45°   ⇒

ΔCBK - прямоугольный равнобедренный. Тогда

CK = CB/√2 = 8/√2 = 4√2 см

Ответ:    4√2 см