Предмет: Алгебра,
автор: Rogonova
помооогите под г оба
Приложения:
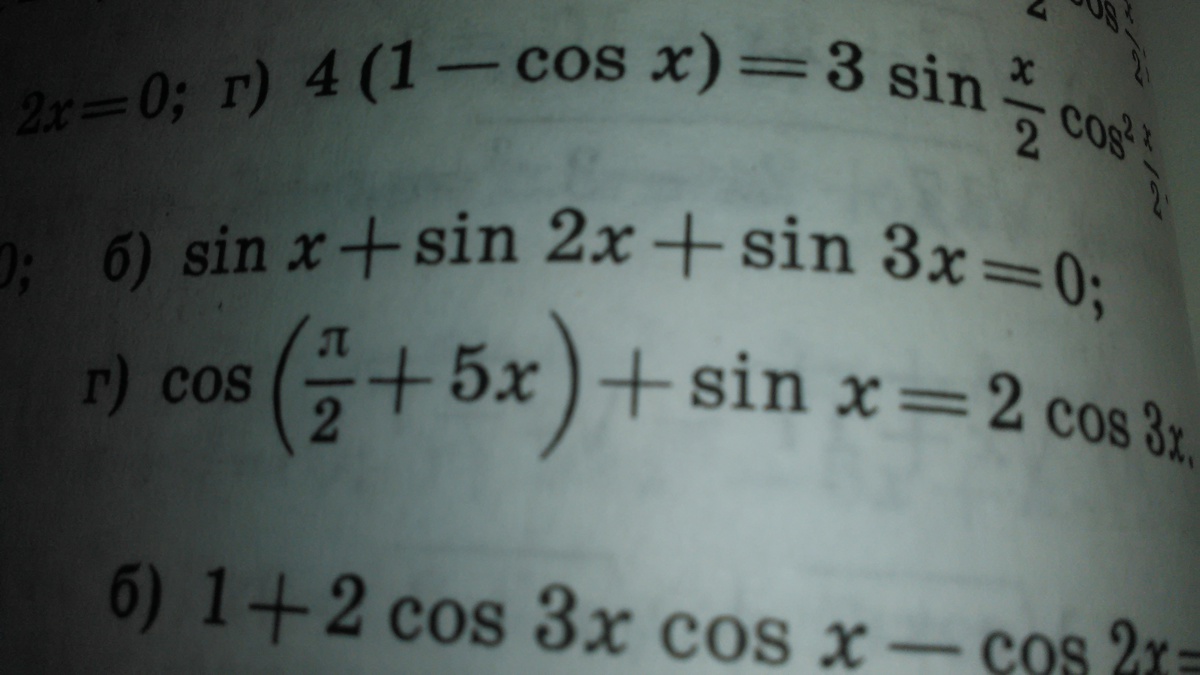
Ответы
Автор ответа:
0
б) sin(x)+sin(2x)+sin(3x) = 0.
Представим sin(3x)+sin3x) = = 2sin((3x+x)/2)*cos((3x-x)/2) =
= 2 sin(2x)*cos(x).
Подставим в исходное уравнение:
2 sin(2x)*cos(x) +sin(2x) = 0
sin(2x)(2cos(x)+1) = 0 по свойству произведения нулю равен один или оба множителя:
sin(2x) = 0
2x = Arc sin 0 = πn+(-1)^n*arc sin 0 = πn
x₁ = πn/2
2cos(x)+1 = 0
cos(x) = -1/2
x₂ = Arc cos (-1/2) = 2πn-+π/6
Представим sin(3x)+sin3x) = = 2sin((3x+x)/2)*cos((3x-x)/2) =
= 2 sin(2x)*cos(x).
Подставим в исходное уравнение:
2 sin(2x)*cos(x) +sin(2x) = 0
sin(2x)(2cos(x)+1) = 0 по свойству произведения нулю равен один или оба множителя:
sin(2x) = 0
2x = Arc sin 0 = πn+(-1)^n*arc sin 0 = πn
x₁ = πn/2
2cos(x)+1 = 0
cos(x) = -1/2
x₂ = Arc cos (-1/2) = 2πn-+π/6
Автор ответа:
0
2cos(3x)(-sin(2x)) = 2cos(3x) после сокращения получаем:
Автор ответа:
0
-sin(2x) = 1 или sin(2x) = -1
Автор ответа:
0
почему именно на -синус5х
Автор ответа:
0
По формуле приведения: cos(Pi/2+x)=-sin(x)
Похожие вопросы
Предмет: Геометрия,
автор: Аноним
Предмет: Физика,
автор: taskabulovamilena7
Предмет: Русский язык,
автор: poshtet
Предмет: Математика,
автор: машкам
Предмет: Математика,
автор: 1цу