Длина стороны квадрата АВСD равна 6 см. Точка М удалена от каждой вершины на 17 см. Найдите расстояние от, середины отрезка МА до середины каждой из сторон квадрата.
Ответы
имеем пирамиду, боковые грани которой - динаковые равнобедренные треугольники с основанием 6 см и боковыми сторонами 17 см,
если у этого треугольника провести высоту, получим два прямоугольных треугольника с меньшим катетом 3 см и гипотенузой 17 м, вспоминаем теорему Пифагора и находим больший катет, который нужен
Ответ:
Расстояние от середины отрезка МА до середин сторон АВ и AD равно ≈ 8,5 см.
Расстояние от середины отрезка МА до середин сторон ВС и СD равно ≈ 9,4cм.
Объяснение:
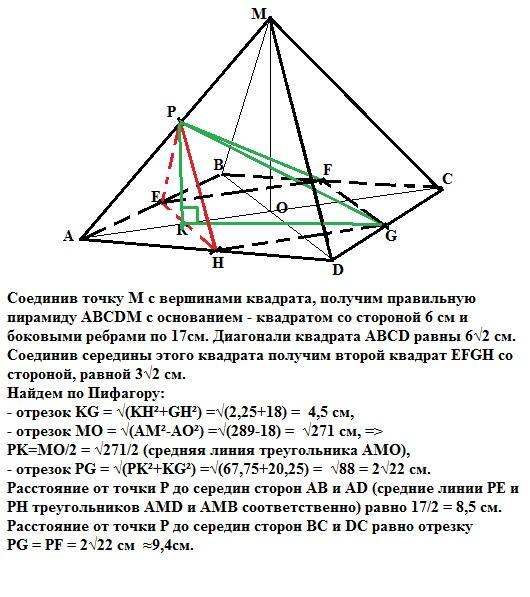
Соединив точку М с вершинами квадрата, получим правильную пирамиду ABCDM с основанием - квадратом со стороной 6 см и боковыми ребрами по 17см. Диагонали квадрата ABCD равны 6√2 см.
Соединив середины этого квадрата получим второй квадрат EFGH со стороной, равной 3√2 см.
Найдем по Пифагору:
- отрезок KG = √(KH²+GH²) =√(2,25+18) = 4,5 см,
- отрезок МО = √(АМ²-АО²) =√(289-18) = √271 см, =>
PK=MO/2 = √271/2 (средняя линия треугольника АМО),
- отрезок РG = √(PK²+KG²) =√(67,75+20,25) = √88 = 2√22 см.
Расстояние от точки Р до середин сторон АВ и AD (средние линии РЕ и РН треугольников AMD и AMB соответственно) равно 17/2 = 8,5 см.
Расстояние от точки Р до середин сторон ВС и DС равно отрезку
PG = PF = 2√22 см ≈ 9,4cм.