Question

Высоты остроугольного треугольника ABC пересекаются в точке H. Известно, что AB=CH. Найдите угол ACB. Ответ запишите в градусах.

Answer 1

Обозначим высоты AD, BE, CF AD = AB sin угла ABC CD = CH sin угла DHC угл DHC=90°-угл DCH= угл ABC тогда AD = AB sin угла ABC = CH sin угла DHC = CD ⇒  угл ACB=45° Ответ: Угол ABC при таком условии найти нельзя

Answer 2

Первый способ:

Достроим ΔАВС до параллелограмма ABEC ⇒ AB = CE = CH

AB || CE, CN⊥AB ⇒ CN⊥CE. Значит, ΔСЕН - прямоугольный и равнобедренный, ∠СЕН = ∠СНЕ = 45°

четыр-ник ВЕСН - вписанный в окружность (∠НВЕ + ∠НСЕ = 180°) ⇒ ∠СЕН = ∠НВС = 45° - опираются на общую дугу СН

В ΔВСК: ∠СВК = 45° ⇒ ∠ВСК = ∠АСВ = 90° - 45° = 45°

Второй способ:

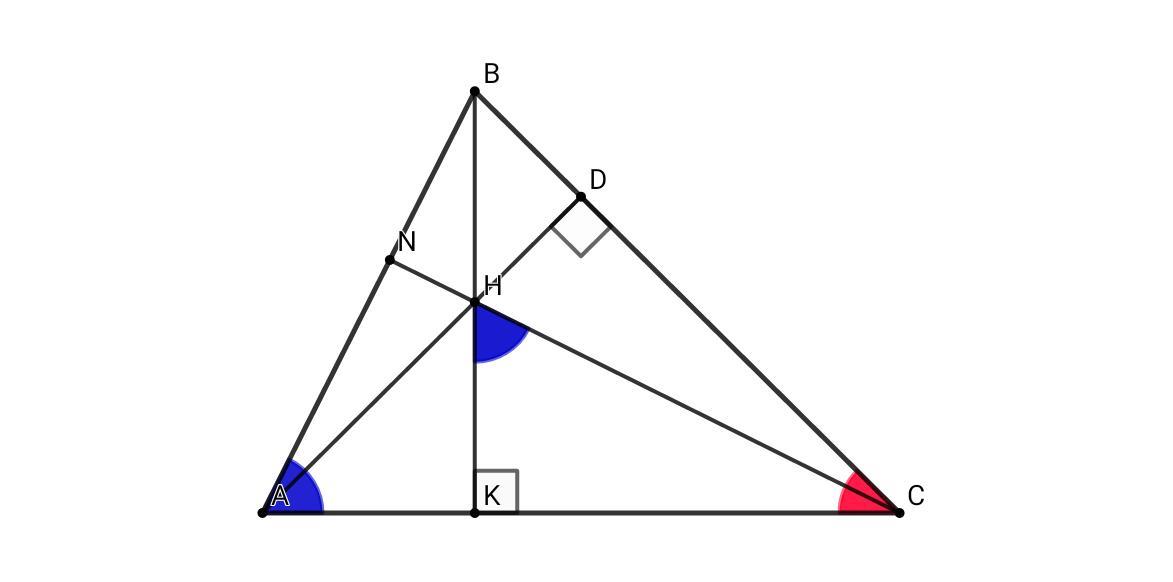
В четыр-ке АNHK: ∠A = 180° - ∠NHK = ∠KHC

В ΔАВК: sin∠A = BK/AB ⇒ BK = AB•sin∠A

B ΔKCH: sin∠KHC = KC/CH ⇒ KC = CH•sin∠KHC

Но АВ = СН, sin∠A = sin∠KHC, значит, ВК = KC ⇒ ΔBСК - прямоугольный и равнобедренный, ∠СВК = ∠ВСК = ∠АСВ = 45°