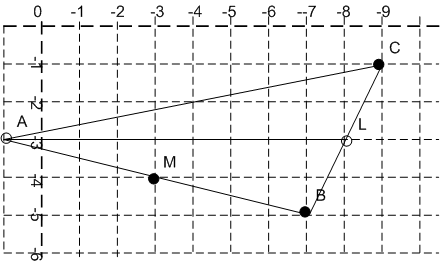
В треугольнике АВС точка М – середина АВ, L – середина ВС, В (– 7; – 5), М (– 3; – 4), С (– 9; – 1). Найдите длину медианы AL.
Ответы
Первое решение - геометрическое.
Строим на тетрадном листике координаты и чертим точки с известными координатами. Так как нам известно, что точи М и L - середины отрезка, то доводим линию BM до точки A и видим, что он оказывается в координатах A(1,-3). Также по чертежу видно, что координаты L(-8.-3). По чертежу выйдет, что AL - прямая линия и ее длина составляет 9 клеток.
Решение по формулам
У нас есть B и С - точка середины отрезка L вычисляется по формуле
L = (B+C)/2.
Lx = (-7 + -9)/2 = -8; Ly= (-5 + -1) / 2 = - 3.
Координаты L(-8.-3).
Если подумать, то отрезок AB с точкой M - тоже вычисляется по этой же формуле:
M = (A + B) / 2.
Отсюда A = 2M - B
Значит
Ax = (2 * (-3)) - (-7) = +1
Ay = (2 * (-4)) - (-5) = - 3
Точка A(1,-3)
Длина отрезка AL = квадратный корень из ((Ax - Lx) ^2 + (Ay - Ly)^2))
AL =квадраткорень( (1- (-8))*(1- (-8)) + (-3- (-3))* (-3- (-3)) = квадраткорень (9*9 - 0*0) = 9
Как-то так.