Предмет: Математика,
автор: sredz96
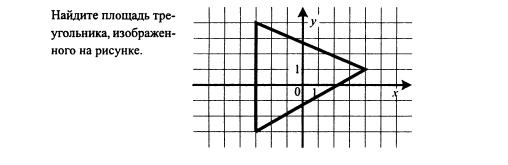
Вопрос к фотографии №3: Найдите точку минимума функции.
Помогите решить, пожалуйста...
Приложения:

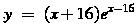
Ответы
Автор ответа:
0
точка минимума-точка где производная меняет знак с минуса на плюс
произв=(x+16)"*e^(x-16)+(x+16)*(e^(x-16)")=1*e^(x-16)+e^(x-16)*x+16*e^(x-16)=e^(x-16)*(1+x+16)=e^(x-16)*(x+17)
приравняем к 0
e^(x-16)*(x+17)=0
тк е не может быть равно 0 в любой степени, то
х+17=0
х= -17
теперь смотрим на промежутках знаки производной
при x< -17 производная меньше 0
при х> -17 производная больше 0
при переходе через точку х= -17, производная поменяла знак с минуса на плюс-значит это точка минимума
другие надо? напиши в комментариях
произв=(x+16)"*e^(x-16)+(x+16)*(e^(x-16)")=1*e^(x-16)+e^(x-16)*x+16*e^(x-16)=e^(x-16)*(1+x+16)=e^(x-16)*(x+17)
приравняем к 0
e^(x-16)*(x+17)=0
тк е не может быть равно 0 в любой степени, то
х+17=0
х= -17
теперь смотрим на промежутках знаки производной
при x< -17 производная меньше 0
при х> -17 производная больше 0
при переходе через точку х= -17, производная поменяла знак с минуса на плюс-значит это точка минимума
другие надо? напиши в комментариях
Похожие вопросы
Предмет: Математика,
автор: zhatoka1986
Предмет: Алгебра,
автор: 72646647373746
Предмет: Физика,
автор: vinogradinka14
Предмет: Алгебра,
автор: ladyprool
Предмет: Алгебра,
автор: Талащеночка