Question

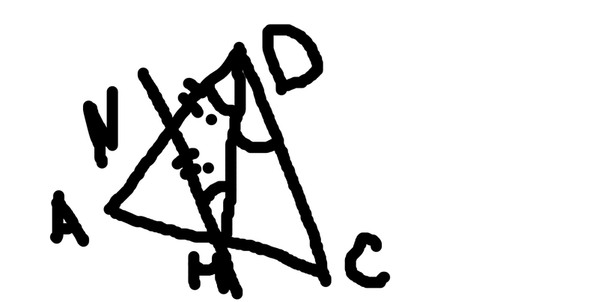
Отрезок DM - биссектриса треугольника АDС. Через точку М проведена прямая параллельная стороне CD и пересекающая сторону DA в точке N. Найдите все углы треуголника DMN, если известно что угол ADC=72 градусам.
помогите плиз!

Answer 1

1) т.к. DM - биссектриса, то она делить угол D на два равных: угол ADM=CDM=36 градусов.
2) т.к. в этой задаче есть параллельные прямые, то всё до жути просто.
при параллельных прямых, пересеченных секущей, накрест лежащие углы равны.
3) тогда при параллельных прямых NM и CD углы CDM=NMD, как накрест лежащие.
4) получается, что углы NDM=NMD=36, отсюда следует, что ΔDMN - равнобедренный.
5) 180-36-36=108 градусов - угол DNM.
ответ: 36; 36, 108.
(криво, косо, некрасиво, но  суть вы поймете)