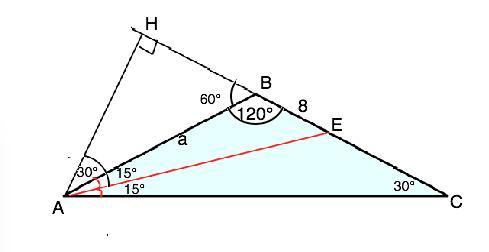
В треугольнике ABC AB = BC, угол CAB = 30 градусов, AE - биссектриса, BE = 8см. Найдите площадь треугольника ABC.
Ребята,помогите пожалуйста,заранее спасибо большое.
Ответы
В треугольнике АВС (АВ=ВС) проведем высоту АН к стороне ВС. Высота тупоугольного треугольника, проведенная из вершины острого угла, лежит вне треугольника.
В равнобедренном ∆ АВС ∠ВСА=∠САВ= 30°,⇒ ∠В=180°-2•30°=120° В Δ АВН угол АВН смежный углу АВС равен 180°-120°=60°. Угол ВАН=180°- 90°-60°=30°.
Примем АВ=ВС равными а. Тогда ВН=а•sin30°=a/2, AH=a•sin60°=a√3/2.
Биссектриса АЕ делит угол ВАС на два по 30°:2=15°. Тогда в прямоугольном треугольнике НАЕ ∠НАЕ=<НАВ+ <ВАЕ=30°+15°=45°. Сумма острых углов прямоугольного треугольника 90°, поэтому ∠НЕА=45°⇒ ∆ АНЕ - прямоугольный равнобедренный (по свойству), и ЕН=АН=a√3/2
НЕ=ВЕ+ВН=(8+а/2 )
Из равенства АН=ЕН следует a√3/2=8+а/2, откуда получим а-8=8√3, ⇒ а=8(√3+1) см
Площадь равнобедренного треугольника равна половине произведения равных сторон на синус угла между ними.
S(ABC)=0,5•a²•sin120°. S(ABC)=0,5•[8(√3+1)]²•√3/2=32√3( 2+√3) см²