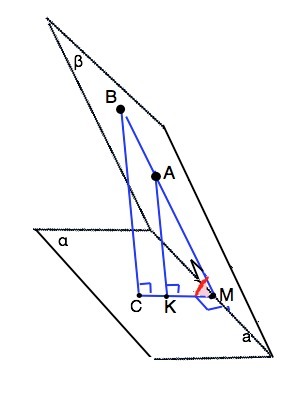
Точки А и В лежат на одной грани двугранного угла.Найдите величину этого угла,если точки А и В удалены от его ребра на 4√2 см и 6√2 см,а сумма расстояний от данных точек до второй грани 10см.
Ответы
Определение 1. Двугранным углом называется фигура, образованная двумя не принадлежащими одной плоскости полуплоскостями, имеющими общую границу – прямую а. Величина двугранного угла равна его линейному углу.
Определение 2. Линейным углом двугранного угла называется угол, сторонами которого являются лучи с общим началом на ребре двугранного угла, которые проведены в его гранях перпендикулярно ребру.
Расстояние от точки до прямой и от точки до плоскости равно длине проведенного между ними перпендикуляра.
Обозначим грани угла α и β, ребро - а Пусть точки А и В лежат в плоскости грани β. Длина перпендикуляра ВМ=6√2, перпендикуляра AM=4√2.
Опустим из т.А и т.В перпендикуляры ВС и АК на грань α. ВМ - наклонная, СМ - ее проекция на плоскости грани α. По т. о 3-х перпендикулярах СМ⊥ребру а. ⇒ Угол ВАС - искомый.
В треугольнике ВМС отрезки АК||ВС, ⇒ острые углы прямоугольных ∆ ВСМ и АМК равны, эти треугольники подобны.
По условию ВС+АК=10 см Примем длину АК=х см. Тогда ВС=10-х см. Из подобия следует отношение х:(10-х)=4√2:6√2, ⇒ х•6√2=(10-x)•4√2. Откуда получим 5х=20 см, х=4 см. Из прямоугольного треугольника АКМ sinAMK=АК:АМ=4:4√2=1/√2, что равно √2/2, – синусу 45°. Величина данного двугранного угла 45°.