Предмет: Геометрия,
автор: melissa17
СРОЧНО!!!!!ДАЮ 68 БАЛЛОВ!!!!
В цилиндре, длина высоты которого равна 5 см, а площадь боковой поверхности 40 (пи) см2, проведены два взаимно перпендикулярных диаметра основания ОК и АД. вычислите длину отрезка, соединяющего центр другого основания с серединой отрезка KD
(пи) см2, проведены два взаимно перпендикулярных диаметра основания ОК и АД. вычислите длину отрезка, соединяющего центр другого основания с серединой отрезка KD
Ответы
Автор ответа:
5
Площадь боковой поверхности цилиндра:
Sбок = 2πR · h,
где R - радиус основания цилиндра, h - его высота.
40π = 2πR · 5
R = 4 см.
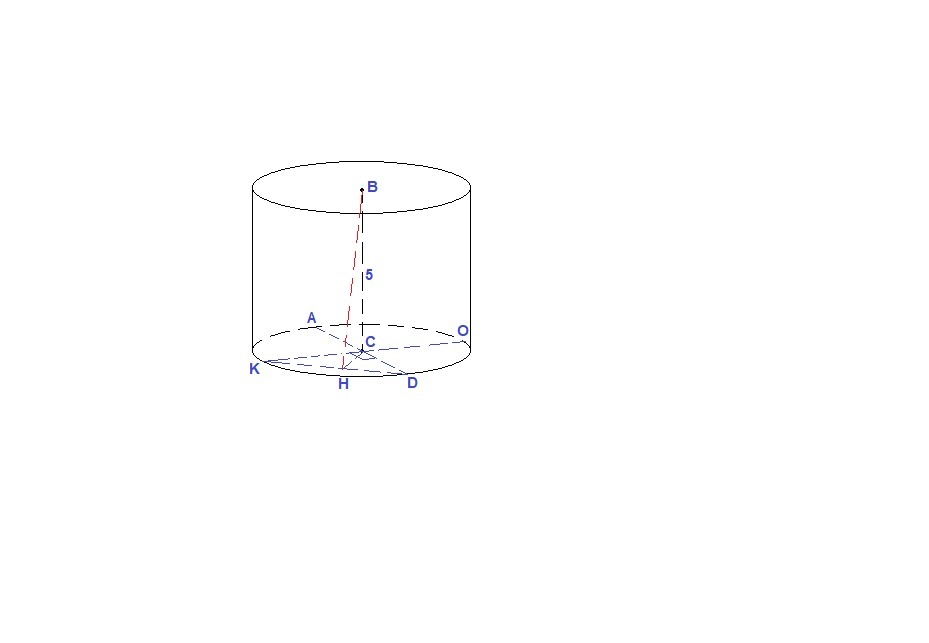
Пусть С - центр нижнего основания, В - центр верхнего.
СК = СD = R = 4 см
ΔCKD - прямоугольный, равнобедренный, значит
KD = CK√2 = 4√2 см.
Пусть Н - середина отрезка KD, тогда СН - медиана и высота ΔCKD, а медиана прямоугольного треугольника, проведенная к гипотенузе, равна ее половине:
СН = KD/2 = 2√2 см
Из прямоугольного треугольника ВСН по теореме Пифагора:
ВН = √(ВС² + СН²) = √(25 + 8) = √33 см
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: Sun77024656
Предмет: Английский язык,
автор: Аноним
Предмет: Английский язык,
автор: mixalich2001
Предмет: Русский язык,
автор: bulavinaviktoria666
Предмет: Русский язык,
автор: vollir98