Предмет: Математика,
автор: Nocomment13
50 баллов. исследовать функцию и построить график помогите

Ответы
Автор ответа:
0
Область определения ![(-infty,3] (-infty,3]](https://tex.z-dn.net/?f=%28-infty%2C3%5D)
Область значений
Производная равна
Поэтому сама функция убывает на интервалах и
и  ,
,
а возрастает на интервале .
.
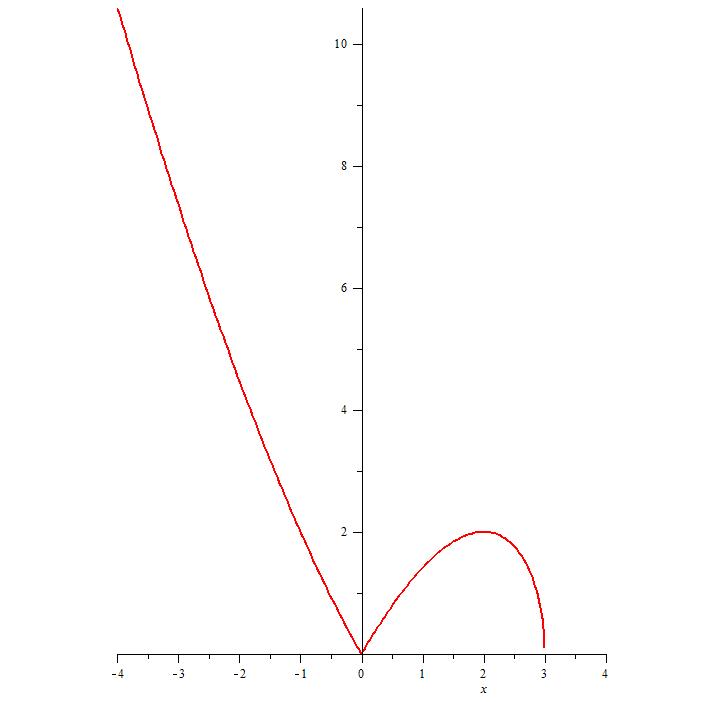
В точках x=0 и x=3 - минимум равный 0.
В точке x=2 - локальный максимум равный 2.
Производная в 0 и 3 не существует. Но есть ее левый предел в 0 равный -
 . и правый
. и правый  . В точке x=3 график входит вертикально, потому что левый предел производной равен бесконечности.
. В точке x=3 график входит вертикально, потому что левый предел производной равен бесконечности.
Область значений
Производная равна
Поэтому сама функция убывает на интервалах
а возрастает на интервале
В точках x=0 и x=3 - минимум равный 0.
В точке x=2 - локальный максимум равный 2.
Производная в 0 и 3 не существует. Но есть ее левый предел в 0 равный -
Приложения:
Автор ответа:
0
вот, сейчас совсем правильно :)
Автор ответа:
0
Так что уголок у графика в нуле равен 60 градусов, так как тангенсы наклона левой и правой касательной в этой точке равны корень из 3.
Автор ответа:
0
пасиб)
Автор ответа:
0
а функция четная или нечетная?)
Автор ответа:
0
ни четная, ни нечетная
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Химия,
автор: Diana81015
Предмет: Физика,
автор: lviktorialap
Предмет: Химия,
автор: Elizabeth21